재미없고 어렵다고? 수학을 책으로 읽어봐

수학을 잘하기 위해선 수학과 관련된 많은 경험을 해보는 것이 필요하다. 교구를 활용한 수학 체험은 수학에 쉽게 다가갈 수 있는 좋은 방법이다. 그러나 추상적 수학 개념이 많이 나오는 중학교 이상 교육과정에서 개념을 구체적 조작으로 학습하기엔 한계가 있다. 개념을 학습하는 데 효과적인 방법은 독서다. 개념이 만들어진 역사적 과정과 그것이 활용된 예를 알면 수학을 더 깊이 이해할 수 있으며, 독서를 통해 얻은 간접 경험은 수학 학습과 동기 부여에 중요한 자극이 된다. 수학 관련 책을 읽으면 개념이나 문제의 배경을 알게 됨으로써 흥미롭게 수학을 즐길 수 있다. 

실제 중학 과정에서 많이 출제되는 문제를 통해 독서가 수학문제를 푸는 데 어떤 도움이 되는지 알아보자. 

이 문제를 해결하는 것은 그리 어렵지 않다. 그러나 단지 배운 개념을 확인하기 위한 문제 해결의 차원을 넘어 더 깊은 이해를 원한다면 독서 활동이 효과적이다. 다음 자료를 보자. 




















 

밑면의 반지름의 길이가 2㎝, 높이가 6㎝인 원기둥이 있다. 밑면의 A 지점에서 원기둥의 옆면을 따라서 한 바퀴 돌아서 B 지점에 이르는 최단 거리를 구하여라. 















 

나팔꽃의 운동 

여름철에는 담장에 피어나는 나팔꽃을 흔히 볼 수 있다. 그 생명이 비록 몇 개월밖에 안 된다 하더라도 나팔꽃은 힘껏 꽃을 피우려 하고 또 좋은 씨를 많이 남기려 한다. 그러려면 되도록 빨리, 멀리 그 줄기를 뻗어야 한다. 다른 식물들에 가리지 않아야 햇빛을 많이 받을 수 있기 때문이다. 그러나 나팔꽃은 줄기가 여려서 혼자서는 지탱하지 못하므로, 다른 나무줄기나 막대기 등을 타고 올라가야 한다. 나팔꽃이 타고 올라가는 나무줄기나 막대기는 원기둥 모양이다. 나팔꽃이 타고 올라가는 모습은 직선이 아닌 곡선 같지만, 잘 살펴보면 흥미로운 사실을 발견할 수 있다. 아래 그림은 나팔꽃이 물체를 타고 올라가는 것을 원기둥 위에 선으로 표시한 것이다. 원기둥의 옆면을 펴면, 타고 올라가는 경로가 실제로는 직선임을 알 수 있다. 이것은 되도록 빨리 뻗어 올라가 햇볕을 받으려는 나팔꽃의 생존 의지를 보여주는 것이다. 

 














 




이 글을 통해 원기둥 최단 거리의 개념이 자연 관찰에서 시작됐다는 것을 알 수 있다. 

이제는 당연하게 여기는 X축과 Y축으로 이루어진 좌표평면의 개념도 데카르트의 이야기가 등장하면 실감나고 재미있는 이야기로 바뀌게 된다. 

병약한 데카르트가 침대에 누워 천장을 바라보다 요리조리 움직이는 파리의 위치를 정확히 표현하기 위해 좌표평면을 그렸다는 사실을 알게 된다면 그 자체로도 수학은 지루한 과목이 아니라 호기심과 재미로 가득 찬 학문이 될 수 있다. 

이처럼 읽기 자료는 실생활 속에 숨어 있는 수학적 현상을 파악할 수 있는 사고력을 키워준다. 또한 이런 배경지식은 수학을 폭넓게 이해하는 데 도움이 되고, 지적 자극을 통해 학습 동기를 부여한다. 









■ 생각해보자 

다음 글을 읽고 물음에 답하시오. 

 



(1) 종이의 가로와 세로의 길이 비가 약 얼마가 돼야 효율적인가? (소수점 아래 3자리까지 답하시오.) 

(2) A4 용지의 가로와 세로의 길이 비를 계산하고 A4 용지가 효율적인 크기인지 판단해보자. 

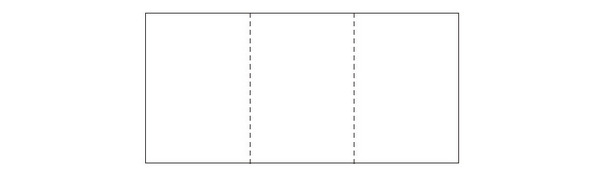
(3) 다음과 같이 큰 종이 한 장을 삼등분하여 작은 종이 세 장을 만들려고 한다. 큰 종이와 작은 종이의 모양이 같도록 하고 싶다면, 종이의 가로와 세로의 길이 비가 얼마가 되도록 해야 하는가? 

 

 한겨레