기하학에서
오일러의 정리란, 삼각형의 외접원의 반지름 R, 내접원의 반지름 r이라 할 때, 외심과 내심의 거리
<math xmlns="http://www.w3.org/1998/Math/MathML" alttext="{\displaystyle d={\sqrt {R^{2}-2Rr}}}"><semantics><annotation encoding="application/x-tex">{\displaystyle d={\sqrt {R^{2}-2Rr}}}</annotation></semantics></math>
이라는 정리이다.
오일러의 정리와 그에 필요한 보조선, 보조점들
증명
삼각형 ABC에 대하여, 외심을 O, 내심을 I라 하고, IO와 외접원의 두 교점을 X,Y라 하고,
호 BC의 중점을 M이라 하고, 직선 MO와 외접원의 M과 다른 교점을 D라 하고, 내접원과 AC의 접점 E라 하자.
<math xmlns="http://www.w3.org/1998/Math/MathML" alttext="{\displaystyle AI*IM=XI*YI=(R+d)(R-d)=R^{2}-d^{2}}"><semantics><annotation encoding="application/x-tex">{\displaystyle AI*IM=XI*YI=(R+d)(R-d)=R^{2}-d^{2}}</annotation></semantics></math>
또한
멘션 정리에 의하여
<math xmlns="http://www.w3.org/1998/Math/MathML" alttext="{\displaystyle IM=BM}"><semantics><annotation encoding="application/x-tex">{\displaystyle IM=BM}</annotation></semantics></math>
<math xmlns="http://www.w3.org/1998/Math/MathML" alttext="{\displaystyle \angle {BDM}=\angle {EAI}}"><semantics><annotation encoding="application/x-tex">{\displaystyle \angle {BDM}=\angle {EAI}}</annotation></semantics></math>
(길이가 같은 두 호 BM,CM의
원주각)
<math xmlns="http://www.w3.org/1998/Math/MathML" alttext="{\displaystyle \angle {DBM}=90^{\circ }=\angle {AEI}}"><semantics><annotation encoding="application/x-tex">{\displaystyle \angle {DBM}=90^{\circ }=\angle {AEI}}</annotation></semantics></math>
즉
<math xmlns="http://www.w3.org/1998/Math/MathML" alttext="{\displaystyle \triangle {DBM}\sim \triangle {AEI}(AA)}"><semantics><annotation encoding="application/x-tex">{\displaystyle \triangle {DBM}\sim \triangle {AEI}(AA)}</annotation></semantics></math>
<math xmlns="http://www.w3.org/1998/Math/MathML" alttext="{\displaystyle AI*BM=DM*IE=2Rr}"><semantics><annotation encoding="application/x-tex">{\displaystyle AI*BM=DM*IE=2Rr}</annotation></semantics></math>
(닮음비)
따라서
<math xmlns="http://www.w3.org/1998/Math/MathML" alttext="{\displaystyle R^{2}-d^{2}=2Rr}"><semantics><annotation encoding="application/x-tex">{\displaystyle R^{2}-d^{2}=2Rr}</annotation></semantics></math>
이 나오고, 이를 정리하면
<math xmlns="http://www.w3.org/1998/Math/MathML" alttext="{\displaystyle d={\sqrt {R^{2}-2Rr}}}"><semantics><annotation encoding="application/x-tex">{\displaystyle d={\sqrt {R^{2}-2Rr}}}</annotation></semantics></math>
가 성립한다.
Wikipedia
 이라는 정리이다.
이라는 정리이다. 이라는 정리이다.
이라는 정리이다.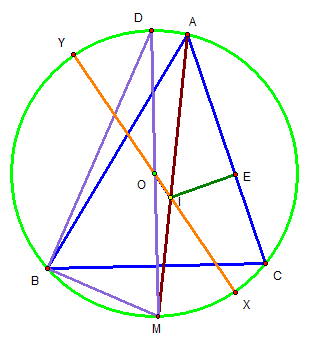



 (길이가 같은 두 호 BM,CM의 원주각)
(길이가 같은 두 호 BM,CM의 원주각)


 (닮음비)
(닮음비) 이 나오고, 이를 정리하면
이 나오고, 이를 정리하면 이 나오고, 이를 정리하면
이 나오고, 이를 정리하면 가 성립한다.
가 성립한다.
댓글 없음:
댓글 쓰기