수학적 사고의 삼두마차 ‘연역·귀납·유추’

하나의 일반적인 사실이나 원리를 전제로 하여 개별적인 사실이나 특수한 다른 원리를 이끌어 내는 것을

 ‘연역’이라고 하고, 연역적으로 논리를 펼쳐 추론을 하는 것을 ‘연역적 추리’라고 한다.

 개별적이고 특수한 사례들로부터 일반적인 원리를 이끌어 내는 귀납적 추리의 방법과 반대의 추론

 방식이다. 예를 들어, ‘3에서 100까지의 다각형을 관찰한 결과 모두 외각의 합이 360˚였다. 

따라서 모든 다각형의 외각의 합은 360˚이다.’는 추론은 귀납이고, ‘다각형의 외각의 합은 360˚이다.

’라는 사실을 근거로 삼아 ‘따라서, 정177각형의 외각의 합도 360˚이다.’라고 결론을 내리는 것은

 연역이다. 




연역의 전제가 되는 사실은 이미 결론의 구체적이고 특수한 경우를 포함하고 있다. 

따라서 전제가 참이고 논리를 전개하는 과정에 오류가 없었다면 결론은 반드시 참이 된다. 

즉, ‘다각형’ 중에는 ‘정177각형’도 포함되어 있기 때문에, 다각형의 외각의 합이 360˚인 

이상 다각형인 정177각형의 외각의 합은 360˚일 수밖에 없다. 따라서 연역적 추론은 결론이 진리임을

 보증해 주는 강력한 논리적 추론 방법이다. 


수학에서 귀납이나 유추적 사고에 의해서 하나의 의미 있는 발견을 해내었다면 연역적 증명으로

 그것이 사실임을 입증하는 절차가 필요하다. 예를 들어, 


은 모두 소수라는 것으로부터

귀납적으로 (n은 0 이상의 정수)은 소수라는 추측을 해볼 수는 있지만,

이것만 가지고는 이 모두 소수라고 결론짓기는 불충분하다. 실제로 이 소수라는 

추측이 나온 지 약 100년 후에 은 641×6700417로 소인수분해되는 합성수임이 밝혀졌다. 


그런데 이렇게 사실임을 확인하는 데는 연역이 필수적이기는 하지만, 연역적 추론은 전제에 

이미 포함되어 있는 결론을 도출해 내는 추론 방식이므로 새로운 것을 발견할 수 없다는 한계가 있다.

 새로운 사실을 발견하기 위해서는 귀납과 유추의 도움이 필요하다. 이렇게 지식을 찾아내는 

추론 방식인 귀납과 유추, 그리고 이것을 확인하는 추론인 연역에 의해서 수학의 체계는 발견되고

완성되어 간다.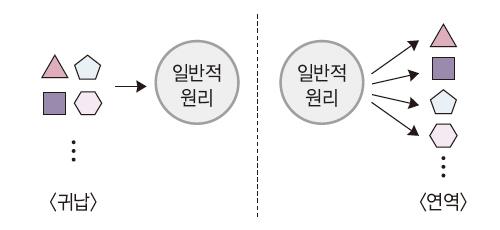 




 






다각형의 외각의 합이 360˚라는 것을 발견하고 증명하는 다음 과정을 보자. 




* 발견의 단계 


［방법 1］ 삼각형을 그려놓고 외각을 각도기로 측정한 후 더해 보았더니 모두 360˚가 되었다. 




［방법 2］ 종이에 다각형을 임의로 그려놓고 외각을 표시하여 잘라낸 후 그것을 모아보았더니 

한 점에 모였다. 한 점의 둘레는 360˚이므로 외각의 합은 360˚이다. 




 




［방법 3］ 원을 여러 개의 부채꼴로 자른 후, 부채꼴을 펼쳐서 내부에 다각형이 생기게 한다.

 이때 부채꼴의 중심각들이 내부에 생긴 다각형의 외각이 되므로 외각의 합은 360˚라고 할 수 있다.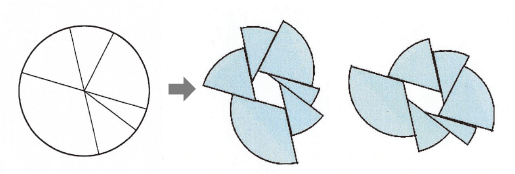 


 




* 증명을 통한 일반화의 단계 


▶ n각형의 한 꼭짓점에서 내각과 외각을 합하면 평각이 되므로 그 값은 180˚이다. …[사실] 


▶ 이러한 꼭짓점이 n개이므로 n각형의 내각과 외각의 합은 180˚×n이다. …[추론] 


▶ n각형의 내각의 합은 (n－2)×180˚이다. …[사실] 


▶ 따라서 다음의 관계가 성립한다. …[추론] 


▶ (n각형의 내각과 외각의 합)=(n각형의 내각의 합)+(n각형의 외각의 합) 


이것을 수식으로 표현하면 180˚×n=(n－2)×180˚＋(n각형의 외각의 합)이다. 


∴(n각형의 외각의 합)=360˚ …[결론] 







 


그런데 초등에서 중등 단계의 학생들은 연역적 추론의 방법을 사용해서 완벽한 증명을 해내는 것이

 힘들 수도 있다. 우선은 문제를 푸는 각 단계마다 연역적 추론의 방법을 사용해 자신의 결론을 

정당화해보는 연습을 하도록 하자. 근거로 사용된 전제는 참인지, 추론 과정이 올바른지를 따져보는 

것이다. 

예를 들어, ‘모든 소수는 홀수이다. 2는 소수이다. 따라서 2는 홀수이다.’라고 했을 때,

 처음 문장이 홀수가 아닌 소수의 

예 2가 있으므로 잘못된 전제로부터 출발하였다. 또 ‘모든 마름모꼴은 선대칭 도형이다. 

수진이는 선대칭 

도형을 그렸다. 따라서 수진이가 그린 도형은 마름모꼴이다.’라는 추론에서는 선대칭 도형을 

그렸다는 

것으로부터 엉뚱하게 마름모꼴을 그렸다는 것으로 결론을 내리고 있다. 

이와 같이 추론에서 잘못이 일어나고 있는 부분이 무엇인지 계속 점검하고 잘못을 바로잡는

 연습은

 완전한 증명을 해내는 밑바탕이 된다. 






■ 생각해보자 




다음 그림과 같이 한 평면에 의해 잘린 정육면체의 단면이 오각형일 때, 오각형의 이웃한 두 변의 

길이의 합이 다른 세 변의 길이의 합보다 큰 두 변이 존재함을 증명해보자.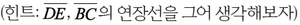 


 


 




한겨레