일반적으로 모든 삼각형과 정다각형들에는 외접원이 존재하지만, 모든 다각형에 외접원이 존재하는 것은 아니다. 정다각형의 경우 외심은 정다각형의 중심과 같다.
삼각형의 외접원]
이것을 증명하려면, 어떠한 변의 수직이등분선은 하나밖에 존재하지 않는다는 것을 이용하여, 두 수직이등분선의 교점에서 나머지 한 변에 내린 수선이 그 변을 이등분한다는 것을 보이면 된다.
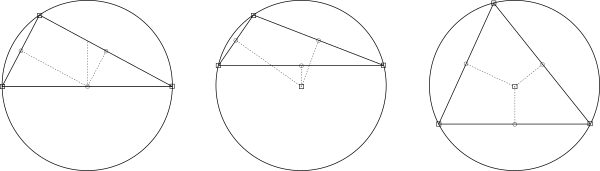
외심의 위치[편집]
외접원과 외심의 성질[편집]
사인 법칙[편집]
삼각형의 세 변의 길이와 세 각의 크기를 각각 라 하고, 외접원의 반지름 길이를 이라 할 때, 이 성립한다.
외접원과 삼각형의 넓이[편집]
삼각형의 세 변의 길이를 라 하고, 외접원의 반지름 길이를 이라 할 때, 삼각형의 넓이 는
이 성립한다.
증명은 다음과 같다.
(삼각형의 넓이) (사인 법칙) 따라서,
우산 정리[편집]
삼각형 와 그 외접원 위의 점 위의 점 에 대해, 다음 세 조건 중 하나를 만족하면 이다.
- 는 각 의 이등분선 위의 점이다.
- 는 한 직선 위에 있으며 이다.
- 는 외심을 지나며 는 와 수직이다.
오일러의 정리[편집]
외접원과 내접원의 반지름 R,r에 대해 내심과 외심 사이 거리는 이다.
오일러의 부등식[편집]
외접원과 내접원의 반지름 R,r에 대해 R은 2r보다 같거나 크다.
사각형의 외접원
사각형 ABCD에 원이 외접하려면 다음 조건 중 하나를 만족하여야 한다.
Wikipedia



























댓글 없음:
댓글 쓰기