조르당 곡선에서 정사각형을 찾아라

시작점과 끝점이 같은 곡선을 볼펜을 떼지 않고 한 번에 이어서 그립니다. 볼펜이 지나간 점은 다시 가지 않도록 조심해서 말이죠. 이렇게 그린 곡선을 수학에서는 ‘조르당 곡선’이라고 합니다.

1911년 독일의 수학자인 오토 퇴플리츠는 조르당 곡선을 생각하다 다음과 같은 질문을 했습니다.

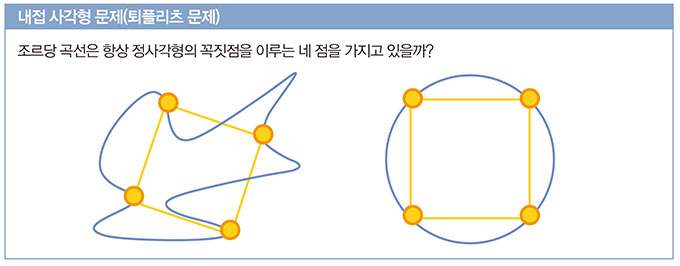
처음에 수학자들은 이 문제가 쉽다고 여겼습니다. 하지만 지금까지도 미해결일 만큼 어려운 문제입니다. 문제 자체는 이해하기 쉬운데, 답을 아무도 모른다니 신기하지 않나요?

미국 수학자 월터 스트롬퀴스트는 1989년 조르당 곡선이 ‘충분히 예쁘게 생겼다면’ 정사각형의 꼭짓점을 이루는 네 점이 반드시 있다는 것을 증명했습니다. 여기서 충분히 예쁘다는 것은 곡선 위의 각각의 점에서 좌표계를 잘 잡으면 그 점 근방에서는 그 곡선이 어떤 증가함수 f(x)의 그래프로 나타난다는 뜻입니다.

이 결과만 보면 ‘문제를 거의 다 푼 게 아니냐’고 생각할 수도 있습니다. 그런데 사실 그렇지 않습니다. 평면에 연속함수로 그림을 그린다고 해도 항상 원하는 만큼 예쁘게 생겼다고 보장할 수는 없거든요. 곡선 중에는 또 조르당 곡선은 매우 신기한 성질을 가지고 있는 것도 있어서 당연해 보이는 것도 수학적으로 증명하는 게 매우 까다롭습니다.

엄밀하게 다루기 까다로운 조르당 곡선

평면에 조르당 곡선이 있을 때 가위로 평면에서 조르당 곡선이 지나간 자리를 다 잘라버리면 평면은 몇 조각으로 나뉘게 될까요? 물론 2조각입니다. ‘조르당 곡선 정리’에 따르면 평면에 있는 조르당 곡선은 평면을 안과 밖 2개의 영역으로 나눕니다. 그런데 이 정리를 증명하는 것은 그리 간단치 않습니다. 조르당 곡선 중에는 미분이 되지 않는 정말 특이한 곡선이 많기 때문입니다.

이 조르당 곡선대로 종이를 가위로 자르면 평면이 한 조각일까 두 조각일까? 조르당 곡선 정리에 의하면 두 조각으로 나뉜다

오죽하면 조르당 곡선 정리를 처음 증명했다고 알려진 프랑스 수학자 카미유 조르당이 1887년 한 증명은 틀렸고, 그 후에 다른 사람이 한 증명만 옳다는 이야기도 떠돌았습니다. 저도 그렇게만 알고 있었는데, 2007년 미국 수학자 토마스 헤일스가 직접 조르당의 증명을 살펴보니 틀린 게 없다고 말했다는 이야기도 있어서 조르당의 증명에 대해 확실하게 말하기는 어렵습니다. 그만큼 조르당 곡선 정리를 증명하고, 검증하는 건 어려운 일입니다. 

어쨌든 조르당 곡선 정리는 워낙 중요해서 많은 수학자가 다양한 방식으로 증명했고, 그것도 완벽하게 확인하기 위해 2007년 헤일스가 이끄는 연구팀은 아예 사람이 아닌 컴퓨터가 확인할 수 있는 증명을 만들기도 했습니다. 

그런데 조르당 곡선의 넓이는 얼마일까요? 곡선이 만드는 내부의 넓이가 아니라 곡선 자체의 ‘넓이’ 말이에요. 곡선의 폭은 0이므로 당연히 0이 아닐까 생각할 겁니다. 하지만 조르당 곡선의 일종인 ‘오스굿 곡선’ 위의 점들을 다 모으면 상식과 다르게 넓이가 0보다 큽니다. 

조르당 곡선의 일종인 오스굿 곡선 위에 점들을 모아 넓이를 구하면 0보다 크다.

이렇게 간단하면서도 복잡한 조르당 곡선에 관한 문제는 어떤 건 쉽게 증명되고, 어떤 건 매우 어려운 문제로 남아있습니다. 사각형을 찾는 문제는 어려운 것 중 하나죠. 정사각형은 100년 넘게 답을 못 찾고 있지만, 직사각형 찾는 문제는 이미 한참 전에 해결됐습니다. 미국 수학자 도로시 본이 위상수학의 방법을 이용해 멋지게 증명했지요.

원하는 모양의 사각형은 없을까?
 

가로세로 비율이 3인 직사각형도 항상 있을까요? 현재 수학자들은 원하는 가로세로 비율이 되는 직사각형도 반드시 있는지 연구를 하고 있습니다. 그래도 좀 어려워서 조르당 곡선 중에 무한 번 미분 가능한 매끄러운 곡선만 가지고 따지기도 합니다.

 

 

그럼 직사각형이나 정사각형 말고 다른 사각형은 어떨까요? 원 역시 조르당 곡선이므로, 만일 임의의 조르당 곡선 위에 어떤 사각형의 네 꼭짓점이 동시에 있을 수 있다면 그 사각형은 반드시 원에 내접하는 사각형이어야 합니다. 그렇다면 반대로 원에 내접하는 사각형을 잘 확대 또는 축소해서 임의의 조르당 곡선 위에 네 꼭짓점이 항상 있게 할 수는 없을까요? 이 문제 역시 대부분 경우 해결되지 않았습니다.

특수한 경우만을 오스트리아 과학기술대학교의 두 수학자 아르제니이 아코퓌안과 세르게이 아바쿠모프가 해결했죠. 두 수학자는 조르당 곡선이 ‘볼록’이라서 안쪽으로 꺾인 부분이 없고, 곡선이 어느 정도 매끄러우면, 임의의 원에 내접하는 사각형을 잘 확대 또는 축소하면 그 곡선 위에 네 꼭짓점이 동시에 올라가도록 할 수 있다는 것을 증명했습니다. 이 논문은 2018년 ‘수학 포럼, 시그마’라는 신생이지만 수준 높은 수학 학술지에 출판됐습니다.

이처럼 매우 간단해 보이는 평면에서의 도형 문제도 아직 미해결인 흥미로운 문제가 많이 있습니다. 아직 아무도 생각하지 않은 더 재미있는 좋은 문제를 만들어보고 풀려고 생각해보면 어떨까요? 그게 바로 수학 연구입니다.

동아사이언스