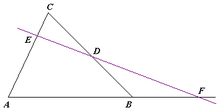
녹원학원 수학과학영재교육 010-3549-5206 : 메넬라오스의 정리 Menelaus' theorem KMO 기하영역 기초정리

2019년 2월 6일 수요일

메넬라우스의 정리. 직선이 삼각형 내부를 지나는 경우.

메넬라우스의 정리. 직선이 삼각형 내부를 지나지 않는 경우.

삼각형 ABC와 각각 직선 BC, CA, AB에 놓인 점 D, E, F에 대하여, 다음 두 조건이 서로 동치이다.

여기서 AF/FB는 부호 있는 비율이며, F가 AB의 내분점이면 양수, 외분점이면 음수를 취한다. 남은 두 비율도 비슷하다.

특징[

체바의 정리는 메넬라오스의 정리와 쌍대를 이룬다.
임의의 다각형에서도 성립한다. 예를 들어, 사각형 ABCD의 네 변 AB, BC, CD, DA 또는 그의 연장선과 직선 l의 교점을 E, F, G, H라 하면 다음이 성립한다.
${\frac {AE}{EB}}\cdot {\frac {BF}{FC}}\cdot {\frac {CG}{GD}}\cdot {\frac {DH}{HA}}=1$
직선이 다각형을 지나지 않아도 된다

증명 도해

D, E, F가 공선점이라고 가정하자. 점 B를 지나 직선 AC의 평행선을 긋고, EF와의 교점을 X라고 하자. 그렇다면, 닮음 삼각형에 따라,

{\frac {AF}{FB}}={\frac {AE}{XB}}

{\frac {BD}{DC}}={\frac {BX}{EC}}

이다. 따라서, 부호를 고려하지 않는다면,

{\frac {AF}{FB}}\cdot {\frac {BD}{DC}}\cdot {\frac {CE}{EA}}={\frac {AE}{XB}}\cdot {\frac {BX}{EC}}\cdot {\frac {CE}{EA}}=1

이다. 또한, 세 비율 가운데, 홀수 개만 음수이므로, 부호를 고려한 곱은 -1이다.

반대로, 비율의 곱이 -1이라고 가정하자. DE의 연장선과 AB의 교점이 G라고 하자. 그렇다면, 위 증명에 따라, G의 내(외)분 비율은 F의 내(외)분 비율과 같으므로, F와 G는 같은 점이다. 따라서, D, E, F는 공선점이다.

AF→ = λAB→, BD→ = μBC→, CE→ = νCA→라 가정하자. B, C, D가 한 직선 상에 있으므로, AD→는 AB→와 AC→에 의해 계수 합이 1이 되도록 분해된다.

{\overrightarrow {AD}}=(1-\mu ){\overrightarrow {AB}}+\mu {\overrightarrow {AC}}

이에 앞서 가정한 것들을 대입하면

{\overrightarrow {AD}}={\frac {1-\mu }{\lambda }}{\overrightarrow {AF}}+{\frac {\mu }{1-\nu }}{\overrightarrow {AE}}

그러므로 D, E, F가 공선점임은, 다음 일련의 조건들과 각각 동치이다.

계수의 합이 여전히 1이다. 즉
${\frac {1-\mu }{\lambda }}+{\frac {\mu }{1-\nu }}=1$
AF/FB, BD/DC, CE/EA를 각각 λ ', μ ', ν '이라 할 때,
${\frac {1-{\frac {\mu '}{1+\mu '}}}{\frac {\lambda '}{1+\lambda '}}}+{\frac {\frac {\mu '}{1+\mu '}}{1-{\frac {\nu '}{1+\nu '}}}}=1$
$\lambda '\mu '\nu '=-1$
$$
$ Wikipedia$