완벽한 파티 만드는 '램지 수'

파티에 손님을 초대하려고 합니다. 서로 아는 사람과 모르는 사람의 수는 어느 정도 돼야 모두가 편안하고 즐거운 분위기에서 파티를 즐길 수 있을까요. 일명 ‘파티 문제’라고 불리는 ‘램지 수’ 연구에서 새로운 결과가 나왔습니다.

램지 수란 서로 친구인 사람의 수를 k, 서로 모르는 사람의 수를 t라 할 때 k명 또는 t명이 반드시 있으려면 최소 몇 명이 있어야 하는지 나타낸 수로 R(k, t)로 나타냅니다. 1930년 영국 수학자 프랭크 램지가 발표한 램지 정리에 따라 언제나 답이 있지만, k와 t 값이 커지면 따져야 할 경우의 수가 많아 아직 정확한 답을 구할 뾰족한 방법을 찾지 못하고 있습니다.

고등과학원 김정한 교수는 램지 수에 대한 업적으로 아시아 최초로 ‘풀커슨상’을 받았습니다. 풀커슨상이란 미국수학회와 수학적 프로그래밍학회에서 3년에 한 번 이산수학 분야에서 가장 뛰어난 논문을 쓴 사람에게 주는 상입니다. 김 교수는 램지 수 R(3,t)에서 t가 커질 때 어떤 속도로 커지는지 정확히 밝힌 공로로 1997년 풀커슨상을 받았습니다.

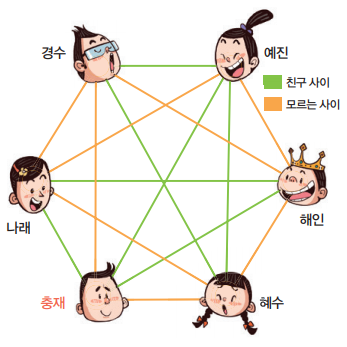
앞의 문제는 램지 수의 가장 간단한 경우 중 하나로, 답은 6명입니다. 그중 한 명의 이름을 충재라고 가정하면 나머지 사람 5명 중 충재의 친구가 3명 이상이거나 충재와 친구가 아닌 사람이 3명 이상일 겁니다. 대칭성이 있으니 충재의 친구가 3명 이상인 경우만 생각해도 되겠죠? 충재의 친구 중 3명을 나래, 해인, 예진이라고 합시다. 만일 나래, 해인이가 서로 친구 사이라면 충재, 해인, 나래는 서로 친구 사이인 세 명이 됩니다(그림).

물론 해인과 나래가 서로 모르는 사이라고 생각해도 됩니다. 그러면 나래와 예진, 예진과 해인이도 서로 모르는 사이라서 나래, 해인, 예진이가 서로 모르는 사이가 돼 이 문제를 풀게 됩니다. 

일러스트 김윤재

김 교수의 업적 중 하나인 R(3,t)은 N명 중에는 반드시 서로 친구 사이인 3명이나 친구 사이가 아닌 t명이 있을 최소의 N값을 뜻한다. 앞에 든 예에 따르면 t=3일때 6명이면 반드시 그런 경우가 있으니 R(3,t)≤6이 됩니다. 5명일 때는 그런 일이 없을 때가 있어 R(3,t)=6입니다.
 

하지만 실제 R(3,t)가 저 속도로 증가하는지는 김정한 교수 연구 이전에는 아무도 알지 못했습니다. 1995년 김정한 교수는 반대 방향의 부등식을 증명합니다. 이 업적으로 김 교수는 1997년에 풀커슨상을 받았습니다. 몇 년 전에 미국 수학자 조엘 스펜서가 R(3,t)의 연구 역사를 소개하는 강연을 하는 것을 들었었는데, 김 교수의 결과를 소개하면서 헝가리 사람이 아니라서 놀랐다고 말하기도 했습니다. 사실 램지 수 연구는 헝가리 수학자들에 의해 활발하게 진행됐습니다. 1930년대 헝가리 수학자인 에르되시 팔과 세케레시 죄르지가 램지 수에 관련된 논문을 내면서 헝가리 수학계에 널리 알려졌거든요.

검증 기간만 6년, 그만큼 어렵고 중요해

지난 2003년 2월 이 부등식에 붙은 라는 상수를 개선한 결과가 거의 비슷한 시기에 두 연구 그룹에서 나왔습니다. 두 팀 모두 같은 결과를 냈고 그 내용은 다음과 같습니다.

인터넷 논문 공개 사이트인 아카이브(arXiv)에 2013년 2월 24일 톰 보먼과 피터 키바쉬는 52쪽짜리 논문을, 이어 다음날 곤찰로 피츠 폰티페로스, 사이먼 그리피스, 로버트 모리스가 쓴 118쪽짜리 논문을 공개했습니다. 

118쪽짜리 논문을 쓴 사이먼 그리피스가 2016년 12월 영국 랜덤 그래프 워크숍에서 자신의 연구를 소개하고 있다. Maths LSE

우연의 일치는 아닌 것 같습니다. 두 그룹이 서로의 연구결과를 알고 있었고, 증명 방법이 달라 논문을 합치지 않은 것으로 생각됩니다. 왜냐하면, 각자 논문에서 상대방의 연구 결과를 언급하고 있기 때문입니다. 

워낙 긴 논문이고 중요한 내용이라 검증 과정이 오래 걸렸습니다. 6년이 지난 2018년에서야 118쪽짜리 논문이 미국수학회에서 발행하는 학술지 ‘미국수학회록’의 심사를 통과했습니다. 

R(3,t) 값이 크다는 것을 증명하려면 서로 아는 세 명도 없으면서 서로 모르는 t명이 없는 경우를 찾아야 합니다. 실제로 손으로 그걸 직접 만들려고 하면 쉽지 않습니다. 이번 연구의 증명을 위해서는 확률을 매우 깊게 사용합니다. 그런데 단순하게 친구 사이를 결정하는 것을 확률로 한다고 해서 좋은 부등식이 나오지는 않습니다. 확률을 사용할 뿐 아니라 다른 아이디어도 잘 섞어야 비로소 좋은 부등식이 얻어집니다.

사실 램지 수로 생각할 수 있는 많은 수열 중에 R(3,t)만큼 증가 속도를 정확하게 알아낸 것이 거의 없을 만큼 램지 수의 연구가 어렵습니다. 그런데 거기에 붙은 상숫값을 이렇게나 많이 정밀하게 구할 수 있다는 것 또한 놀라운 일입니다. 우리가 알아낼 수 있다는 게 놀랍고, 그 한계가 어디까지인지 궁금합니다.

 동아사이언스