원소, 특별한 경우, 그리고 관련 개념[편집]

정팔면체는 세 면에 정사면체를 붙여서 삼각 절두체로 만들 수 있다
각 평면의 부분은 절두체의 바닥이나 밑면이다. 축이 있다면, 이것은 원본인 원뿔이나 각뿔의 축이다. 원형 밑면을 가지면 그 절두체는 원형이다; 축이 양 면에 수직하면 이것은 직 절두체이고 아니면 빗 절두체이다.
절두체의 높이는 두 밑면의 평면의 수직거리이다.
원뿔과 각뿔은 절단면이
꼭대기를 지나는(밑면이 점으로 줄어든) 절두체의 축퇴된 경우로 볼 수 있다. 각뿔 절두체는
기둥형 다면체의 부분 그룹이다.
- <math xmlns="http://www.w3.org/1998/Math/MathML" alttext="{\displaystyle V={\frac {1}{3}}h(a^{2}+ab+b^{2}).}"><semantics><annotation encoding="application/x-tex">{\displaystyle V={\frac {1}{3}}h(a^{2}+ab+b^{2}).}</annotation></semantics></math>

여기서 a와 b는 깎은 각뿔의 밑면과 윗면의 변의 길이이고, h는 높이이다. 이집트인들은 깎은 정사각뿔의 부피를 얻는 공식을 알았지만, 모스크바 파피루스에서 주어진 이 공식에 대한 증명은 없다.
원뿔 또는 각뿔 절두체의
부피는 잘라내기 전의 입체의 부피에서 꼭대기의 부피를 뺀 것이다:
- <math xmlns="http://www.w3.org/1998/Math/MathML" alttext="{\displaystyle V={\frac {h_{1}B_{1}-h_{2}B_{2}}{3}}}"><semantics><annotation encoding="application/x-tex">{\displaystyle V={\frac {h_{1}B_{1}-h_{2}B_{2}}{3}}}</annotation></semantics></math>

이 때 B1은 밑면의 넓이이고, B2는 다른 밑면의 넓이이며, h1, h2 는 꼭대기로부터 각각의 밑면까지의 수직거리이다.
다음을 고려하자
- <math xmlns="http://www.w3.org/1998/Math/MathML" alttext="{\displaystyle {\frac {B_{1}}{h_{1}^{2}}}={\frac {B_{2}}{h_{2}^{2}}}={\frac {\sqrt {B_{1}B_{2}}}{h_{1}h_{2}}}=\alpha }"><semantics><annotation encoding="application/x-tex">{\displaystyle {\frac {B_{1}}{h_{1}^{2}}}={\frac {B_{2}}{h_{2}^{2}}}={\frac {\sqrt {B_{1}B_{2}}}{h_{1}h_{2}}}=\alpha }</annotation></semantics></math>

부피의 공식은 비례 상수 α/3와
h1과
h2 세제곱의 차의 곱 만으로 표현할 수 있다.
- <math xmlns="http://www.w3.org/1998/Math/MathML" alttext="{\displaystyle V={\frac {h_{1}ah_{1}^{2}-h_{2}ah_{2}^{2}}{3}}={\frac {a}{3}}(h_{1}^{3}-h_{2}^{3})}"><semantics><annotation encoding="application/x-tex">{\displaystyle V={\frac {h_{1}ah_{1}^{2}-h_{2}ah_{2}^{2}}{3}}={\frac {a}{3}}(h_{1}^{3}-h_{2}^{3})}</annotation></semantics></math>

두 세제곱의 차를 인수분해 해서 ( a3 - b3 = (a-b)(a2 + ab + b2) ) 절두체의 높이 h1−h2 = h를 얻을 수 있고 α(h12 + h1h2 + h22)/3을 얻을 수 있다.
α를 분배하고 그 정의를 대입하면, 넓이
B1과
B2의
헤론 평균을 얻을 수 있다. 따라서 다른 공식은 다음과 같다:
- <math xmlns="http://www.w3.org/1998/Math/MathML" alttext="{\displaystyle V={\frac {h}{3}}(B_{1}+{\sqrt {B_{1}B_{2}}}+B_{2})}"><semantics><annotation encoding="application/x-tex">{\displaystyle V={\frac {h}{3}}(B_{1}+{\sqrt {B_{1}B_{2}}}+B_{2})}</annotation></semantics></math>

헤론은 이 식을 도출하는데 주목하고 그 가운데 마이너스 일의 제곱근인
허수와 마주하게 되었다.
[2]
특히, 원형 원뿔 절두체의 부피는 다음과 같다:
- <math xmlns="http://www.w3.org/1998/Math/MathML" alttext="{\displaystyle V={\frac {\pi h}{3}}(R_{1}^{2}+R_{1}R_{2}+R_{2}^{2})}"><semantics><annotation encoding="application/x-tex">{\displaystyle V={\frac {\pi h}{3}}(R_{1}^{2}+R_{1}R_{2}+R_{2}^{2})}</annotation></semantics></math>

여기서
π는 3.14159265...,이고
R1,
R2는 두 밑면의
반지름이다.
밑면이 정n각형인 각뿔 절두체의 부피는 다음과 같다:
- <math xmlns="http://www.w3.org/1998/Math/MathML" alttext="{\displaystyle V={\frac {nh}{12}}(a_{1}^{2}+a_{1}a_{2}+a_{2}^{2})\cot {\frac {\pi }{n}}}"><semantics><annotation encoding="application/x-tex">{\displaystyle V={\frac {nh}{12}}(a_{1}^{2}+a_{1}a_{2}+a_{2}^{2})\cot {\frac {\pi }{n}}}</annotation></semantics></math>

여기서 a1과 a2는 두 밑면의 변의 수이다.
<math xmlns="http://www.w3.org/1998/Math/MathML" alttext="{\displaystyle {\begin{aligned}{\text{옆 면 표 면 적}}&=\pi (R_{1}+R_{2})s\\&=\pi (R_{1}+R_{2}){\sqrt {(R_{1}-R_{2})^{2}+h^{2}}}\end{aligned}}}"><semantics><annotation encoding="application/x-tex">{\displaystyle {\begin{aligned}{\text{옆 면 표 면 적}}&=\pi (R_{1}+R_{2})s\\&=\pi (R_{1}+R_{2}){\sqrt {(R_{1}-R_{2})^{2}+h^{2}}}\end{aligned}}}</annotation></semantics></math><math xmlns="http://www.w3.org/1998/Math/MathML" alttext="{\displaystyle {\begin{aligned}{\text{총 표 면 적}}&=\pi ((R_{1}+R_{2})s+R_{1}^{2}+R_{2}^{2})\\&=\pi ((R_{1}+R_{2}){\sqrt {(R_{1}-R_{2})^{2}+h^{2}}}+R_{1}^{2}+R_{2}^{2})\end{aligned}}}"><semantics><annotation encoding="application/x-tex">{\displaystyle {\begin{aligned}{\text{총 표 면 적}}&=\pi ((R_{1}+R_{2})s+R_{1}^{2}+R_{2}^{2})\\&=\pi ((R_{1}+R_{2}){\sqrt {(R_{1}-R_{2})^{2}+h^{2}}}+R_{1}^{2}+R_{2}^{2})\end{aligned}}}</annotation></semantics></math> 고, s는 절두체의 모선 길이이다.
밑면이 닯은
n각형인 직 절두체의 표면적은 아래와 같다:
- <math xmlns="http://www.w3.org/1998/Math/MathML" alttext="{\displaystyle A={\frac {n}{4}}\left[(a_{1}^{2}+a_{2}^{2})\cot {\frac {\pi }{n}}+{\sqrt {(a_{1}^{2}-a_{2}^{2})^{2}\sec ^{2}{\frac {\pi }{n}}+4h^{2}(a_{1}+a_{2})^{2}}}\right]}"><semantics><annotation encoding="application/x-tex">{\displaystyle A={\frac {n}{4}}\left[(a_{1}^{2}+a_{2}^{2})\cot {\frac {\pi }{n}}+{\sqrt {(a_{1}^{2}-a_{2}^{2})^{2}\sec ^{2}{\frac {\pi }{n}}+4h^{2}(a_{1}+a_{2})^{2}}}\right]}</annotation></semantics></math>
![{\displaystyle A={\frac {n}{4}}\left[(a_{1}^{2}+a_{2}^{2})\cot {\frac {\pi }{n}}+{\sqrt {(a_{1}^{2}-a_{2}^{2})^{2}\sec ^{2}{\frac {\pi }{n}}+4h^{2}(a_{1}+a_{2})^{2}}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/cfe2ca30c9417908ab3b1e7cacd952dd58ac0283)
여기서 a1과 a2는 두 밑면의 변의 갯수이다.
예시
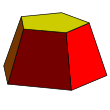

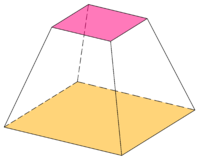









![{\displaystyle A={\frac {n}{4}}\left[(a_{1}^{2}+a_{2}^{2})\cot {\frac {\pi }{n}}+{\sqrt {(a_{1}^{2}-a_{2}^{2})^{2}\sec ^{2}{\frac {\pi }{n}}+4h^{2}(a_{1}+a_{2})^{2}}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/cfe2ca30c9417908ab3b1e7cacd952dd58ac0283)
댓글 없음:
댓글 쓰기