스튜어트의 정리 Stewart's theorem KMO 기하학 기초

스튜어트의 정리(Stewart's theorem)는 삼각형을 구성하는 선분들의 길이에 관한 식이다. 스코틀랜드의 수학자 매튜 스튜어트의 이름을 땄다.

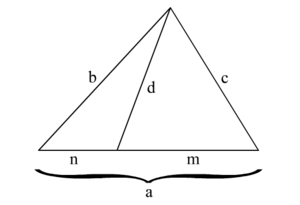
스튜어트 정리]

<math xmlns="http://www.w3.org/1998/Math/MathML" alttext="{\displaystyle a,b,c}"><semantics><annotation encoding="application/x-tex">{\displaystyle a,b,c}</annotation></semantics></math>는 삼각형의 세 변의 길이라고 하고, <math xmlns="http://www.w3.org/1998/Math/MathML" alttext="{\displaystyle d}"><semantics><annotation encoding="application/x-tex">{\displaystyle d}</annotation></semantics></math>는 변 <math xmlns="http://www.w3.org/1998/Math/MathML" alttext="{\displaystyle a}"><semantics><annotation encoding="application/x-tex">{\displaystyle a}</annotation></semantics></math>와 그 반대편의 꼭짓점을 잇는 선분의 길이라고 하자. <math xmlns="http://www.w3.org/1998/Math/MathML" alttext="{\displaystyle d}"><semantics><annotation encoding="application/x-tex">{\displaystyle d}</annotation></semantics></math>가 변 <math xmlns="http://www.w3.org/1998/Math/MathML" alttext="{\displaystyle a}"><semantics><annotation encoding="application/x-tex">{\displaystyle a}</annotation></semantics></math>를 길이 <math xmlns="http://www.w3.org/1998/Math/MathML" alttext="{\displaystyle n}"><semantics><annotation encoding="application/x-tex">{\displaystyle n}</annotation></semantics></math>, <math xmlns="http://www.w3.org/1998/Math/MathML" alttext="{\displaystyle m}"><semantics><annotation encoding="application/x-tex">{\displaystyle m}</annotation></semantics></math>으로 나눈다고 하면, 다음 관계가 성립한다.

<math xmlns="http://www.w3.org/1998/Math/MathML" alttext="{\displaystyle b^{2}m+c^{2}n=a(d^{2}+mn)\,}"><semantics><annotation encoding="application/x-tex">{\displaystyle b^{2}m+c^{2}n=a(d^{2}+mn)\,}</annotation></semantics></math>

특히 <math xmlns="http://www.w3.org/1998/Math/MathML" alttext="{\displaystyle m=n}"><semantics><annotation encoding="application/x-tex">{\displaystyle m=n}</annotation></semantics></math>일 경우 <math xmlns="http://www.w3.org/1998/Math/MathML" alttext="{\displaystyle d}"><semantics><annotation encoding="application/x-tex">{\displaystyle d}</annotation></semantics></math>는 중선이 되고 이때 관계식은 아폴로니우스의 중선 정리가 된다.

증명

<math xmlns="http://www.w3.org/1998/Math/MathML" alttext="{\displaystyle \theta }"><semantics><annotation encoding="application/x-tex">{\displaystyle \theta }</annotation></semantics></math>는 <math xmlns="http://www.w3.org/1998/Math/MathML" alttext="{\displaystyle m}"><semantics><annotation encoding="application/x-tex">{\displaystyle m}</annotation></semantics></math>과 <math xmlns="http://www.w3.org/1998/Math/MathML" alttext="{\displaystyle d}"><semantics><annotation encoding="application/x-tex">{\displaystyle d}</annotation></semantics></math>가 이루는 각이고, <math xmlns="http://www.w3.org/1998/Math/MathML" alttext="{\displaystyle \theta '}"><semantics><annotation encoding="application/x-tex">{\displaystyle \theta '}</annotation></semantics></math>는 <math xmlns="http://www.w3.org/1998/Math/MathML" alttext="{\displaystyle n}"><semantics><annotation encoding="application/x-tex">{\displaystyle n}</annotation></semantics></math>과 <math xmlns="http://www.w3.org/1998/Math/MathML" alttext="{\displaystyle d}"><semantics><annotation encoding="application/x-tex">{\displaystyle d}</annotation></semantics></math>가 이루는 각이라 하자. 두 각을 합하면 180도 이므로 코사인의 성질 때문에 <math xmlns="http://www.w3.org/1998/Math/MathML" alttext="{\displaystyle \cos \theta '=-\cos \theta }"><semantics><annotation encoding="application/x-tex">{\displaystyle \cos \theta '=-\cos \theta }</annotation></semantics></math>이다. 제 2코사인 법칙에 의해 다음 식이 성립한다.

<math xmlns="http://www.w3.org/1998/Math/MathML" alttext="{\displaystyle {\begin{aligned}c^{2}&=m^{2}+d^{2}-2dm\cos \theta \\b^{2}&=n^{2}+d^{2}-2dn\cos \theta '\\&=n^{2}+d^{2}+2dn\cos \theta .\,\end{aligned}}}"><semantics><annotation encoding="application/x-tex">{\displaystyle {\begin{aligned}c^{2}&=m^{2}+d^{2}-2dm\cos \theta \\b^{2}&=n^{2}+d^{2}-2dn\cos \theta '\\&=n^{2}+d^{2}+2dn\cos \theta .\,\end{aligned}}}</annotation></semantics></math>

첫 번째 식에 <math xmlns="http://www.w3.org/1998/Math/MathML" alttext="{\displaystyle n}"><semantics><annotation encoding="application/x-tex">{\displaystyle n}</annotation></semantics></math>을 곱하고, 두 번째 식에 <math xmlns="http://www.w3.org/1998/Math/MathML" alttext="{\displaystyle m}"><semantics><annotation encoding="application/x-tex">{\displaystyle m}</annotation></semantics></math>을 곱하여 더해서 <math xmlns="http://www.w3.org/1998/Math/MathML" alttext="{\displaystyle \cos \theta }"><semantics><annotation encoding="application/x-tex">{\displaystyle \cos \theta }</annotation></semantics></math>를 제거하면 다음을 얻는다.

<math xmlns="http://www.w3.org/1998/Math/MathML" alttext="{\displaystyle {\begin{aligned}&b^{2}m+c^{2}n\\&=nm^{2}+n^{2}m+(m+n)d^{2}\\&=(m+n)(mn+d^{2})\\&=a(mn+d^{2})\\\end{aligned}}}"><semantics><annotation encoding="application/x-tex">{\displaystyle {\begin{aligned}&b^{2}m+c^{2}n\\&=nm^{2}+n^{2}m+(m+n)d^{2}\\&=(m+n)(mn+d^{2})\\&=a(mn+d^{2})\\\end{aligned}}}</annotation></semantics></math>

코사인 법칙을 이용하지 않은 증명도 있다. 수선의 발을 내리고 피타고라스의 정리를 여러번 사용하면 된다.

Wikipedia