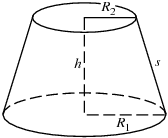Conical Frustum 절두체 부피

A conical frustum is a frustum created by slicing the top off a cone (with the cut made parallel to the base). For a right circular cone, let 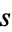 be the slant height 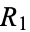and  and 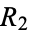 the base and top radii. Then

(1)

The surface area, not including the top and bottom circles, is

			(2)
			(3)

The volume of the frustum is given by

(4)

But

(5)

so

			(6)
			(7)
			(8)

This formula can be generalized to any pyramid by letting 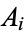 be the base areas of the top and bottom of the frustum. Then the volume can be written as

(9)

The area-weighted integral of 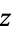 over the frustum is

			(10)
			(11)

so the geometric centroid is located along the z-axis at a height

			(12)
			(13)

(Eshbach 1975, p. 453; Beyer 1987, p. 133; Harris and Stocker 1998, p. 105). The special case of the cone is given by taking 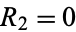, yielding .

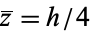Wolfram