선생님이 여러분처럼 초등학생이던 시절에는 가장 손꼽아 기다리던 학교 행사가 운동회였어요. 그때에는 거의 모든 학교가 10월에 운동회를 했지요. 요즘 운동회는 예전과 많이 달라진 것 같아요. 운동장이 작아 저학년은 오전, 고학년은 오후로 운동회를 나눠 하기도 하고 운동회를 아예 하지 않는 경우도 있다고 해요. 또 예전과 달리 많은 학교들이 가정의 달인 5월에 운동회를 열고 있지요. 대구 지역에선 올봄에 운동회를 연 학교가 전체의 85%나 된다고 하네요. 그래서 오늘은 운동회와 관련 있는 내용으로 수학 공부를 하려고 해요.
학교 옥상에서 운동장 바닥까지 만국기 달기
"청군 이겨라! 백군 이겨라!" 학생들이 소리 높여 응원하는 오늘은 신나는 운동회 날이에요. 운동회에 빠질 수 없는 것 중 하나는 하늘에 펄럭거리는 만국기(萬國旗)겠죠? 만국기는 여러 나라의 국기를 줄에 매달아 놓은 것인데, 운동회뿐 아니라 각종 행사에서도 많이 볼 수 있어요.
우리 운동회에서도 이 만국기를 건물 옥상에서 운동장 끝까지 줄에 매달아 드리우려고 해요. 학교 건물 높이는 10m고, 건물 바닥부터 운동장 끝까지 직선거리는 50m예요. 그런데 만국기를 매단 줄의 길이가 51m밖에 안 되네요! 아무리 생각해도 만국기를 학교 옥상에서 운동장까지 늘어뜨리기엔 줄이 짧은 것 같아요. 비스듬히 멋지게 늘어뜨린 만국기 아래로 청·백군 선수들이 멋지게 입장할 계획이었는데, 어쩌면 좋지요? 그렇다고 건물 옥상이 아니라 낮은 곳에 매단다면 모두들 만국기를 허들처럼 뛰어넘거나 그 아래로 기어가야 할지도 몰라요. 그때 선생님께서 만국기가 달린 줄을 들고 가시더니, 학교 옥상에서 운동장 바닥 끝까지 멋지게 매다셨지 뭐에요? 건물 바닥에서 운동장 끝까지 수평으로 줄을 연결해도 50m가 필요한데, 51m밖에 안 되는 만국기 줄을 가지고 어떻게 10m나 되는 건물 옥상부터 운동장 바닥까지 매달 수 있었을까요? 혹시 선생님이 마법이라도 부린 걸까요?
직각 삼각형의 빗변의 길이를 구하면 돼요
자, 이제 그 비밀을 같이 풀어봅시다. 건물 옥상과 바닥, 그리고 만국기를 연결할 운동장 바닥을 선으로 각각 연결해봐요. 그랬더니 어떤 도형이 생기나요? 그렇죠! 평소에 교과서에서 자주 보던 직각 삼각형이 만들어졌네요.
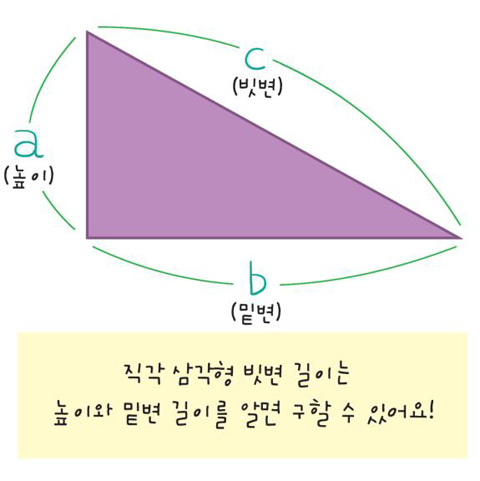
건물 바닥과 운동장 끝을 연결한 선은 직각 삼각형의 '밑변'이 됐고, 건물 바닥에서 옥상까지는 '높이', 옥상에서 운동장 바닥 끝까지 늘어뜨린 만국기는 '빗변'이 됐어요. 여기서 잠깐! 앞으로 직각 삼각형 하면 바로 떠오르게 될 유명한 수학 공식이 있어요. 고대 그리스의 수학자 피타고라스가 처음으로 증명했다는 이것은 무슨 공식일까요? 바로 직각 삼각형에서 빗변의 제곱은 나머지 두 변의 길이의 제곱의 합과 같다는 '피타고라스의 정리'이지요(제곱은 두 번 곱하는 것을 뜻해요). 그럼 일단 길이의 단위 'm'를 빼고 숫자만으로 계산해봐요.
먼저 밑변에 해당하는 건물에서 운동장까지의 길이 50을 거듭 곱하면 '2500'이 나오죠. 그리고 건물 높이 10을 두번 곱하면 '100'이 나옵니다. 피타고라스 정리에 따르면, 이 둘을 더한 것이 옥상에서 운동장까지 길이를 거듭 곱한 것과 같아야겠지요. 정말 그런지 볼까요? 옥상에서 운동장까지 매달 만국기 길이 51을 두번 곱하니 '2601'이 나왔어요. 우와, 오히려 1m가 남네요. 건물 옥상에서 운동장까지 넉넉히 연결할 수 있겠군요. 이제 선생님이 만국기를 문제 없이 매달 수 있었던 비결을 알겠지요?
토너먼트 방식 경기, 결승전까지 남은 게임 수는?
자자, 만국기 문제를 해결했다고 그냥 가버리면 안 되겠죠? 이번엔 운동회에 숨어 있는 또 다른 수학 이야기를 찾아볼게요.
오늘 운동회 종목 중엔 축구와 농구가 있어요. 축구 경기엔 모두 8개 팀이 참가신청을 했어요. 경기 방식은 토너먼트로 하기로 했고요. '토너먼트'는 경기에서 진 팀은 그 즉시 탈락하고 이긴 팀끼리 다음 경기를 치러 차례로 올라가는 방식이지요. 만약 8개 팀이 토너먼트를 한다면 첫 경기에서 4개 팀이 승리해 남게 되고, 다음 경기엔 2개 팀, 마지막 경기에서 우승팀을 가리는 식이에요.
이렇게 토너먼트 방식으로 대회를 열면 총 몇 번 시합을 해야 할까요? 우선, 8개 팀이 토너먼트를 한다고 하면, 처음에 두 팀씩 맞붙어 경기가 총 4번 펼쳐지겠죠? 그리고 남은 네 팀이 2번 경기를 치르고, 마지막으로 결승전을 벌이겠군요. 그럼 총 7번의 경기가 열리게 되겠군요. 만약 16개 팀이 참가하는 토너먼트라면? 8+4+2+1=15, 이렇게 총 15번 경기가 열리는 것이지요. 32개 팀이 참가하면, 16+8+4+2+1=31이니까 총 31번 경기가 열리고…. 음…, 무언가 법칙이 있다는 느낌이 들지 않나요? 맞아요! 토너먼트 참가팀 수에서 1을 빼면 총 경기 수가 나오는 군요.
홀수 팀이 참가하면 부전승 팀이 생겨요
앗! 그런데 농구 경기는 한 팀이 기권해서 7개 팀만 참가한다고 해요. 두 팀씩 맞붙어 3번 경기를 치르게 되고 나머지 한 팀은 상대가 없어 경기를 하지 않겠네요. 이렇게 경기를 치르지 않고도 다음 단계로 진출하는 것을, 싸우지 않고 이겼다는 뜻에서 '부전승(不戰勝)'이라고 해요. 이런 경우에도 토너먼트 총 경기 수는 전체 참가팀에서 1을 뺀 것과 같을까요? 홀수 팀이 참가했으니 앞에서 살펴본 공식과는 달라져야 하지 않을까요?
참가 팀 수가 홀수일 경우엔 어떤지 계산해봅시다. 7개 팀이 나오면 첫 단계에선 3번 경기가 펼쳐지고 한 팀은 부전승으로 올라갑니다. 이렇게 4개 팀이 가려지면 그 다음엔 두팀씩 맞붙어 각각 경기를 치르고 마지막에 결승 경기가 열리지요. 3+2+1=6, 총 여섯 번 경기가 펼쳐지는군요. 홀수 팀이 참가하든, 부전승 팀이 많든 간에 상관없이 토너먼트 총 경기수는 전체 참가 팀에서 1을 뺀 것과 같다는 공식이 성립한답니다. 그럼 무려 1000개의 팀이 토너먼트에 참가했다 하더라도 총 몇 경기가 펼쳐질지 쉽게 알 수 있겠죠? 1000-1=999, 총 999번 경기가 열린답니다.
삐익! 삐익! 토너먼트 경기 수 계산 방법을 알고는 자신만만해 하고 있는데, 우리 팀이 지고 있다는 소식이 들려오네요. 하지만 아직 운동회의 꽃인 '계주 경기'가 남아 있답니다. 펄럭이는 만국기 아래 힘차게 달려 운동회 우승을 거머쥘 거예요!
[관련교과] 3학년 1학기 '평면도형'
학교 옥상에서 운동장 바닥까지 만국기 달기
"청군 이겨라! 백군 이겨라!" 학생들이 소리 높여 응원하는 오늘은 신나는 운동회 날이에요. 운동회에 빠질 수 없는 것 중 하나는 하늘에 펄럭거리는 만국기(萬國旗)겠죠? 만국기는 여러 나라의 국기를 줄에 매달아 놓은 것인데, 운동회뿐 아니라 각종 행사에서도 많이 볼 수 있어요.
우리 운동회에서도 이 만국기를 건물 옥상에서 운동장 끝까지 줄에 매달아 드리우려고 해요. 학교 건물 높이는 10m고, 건물 바닥부터 운동장 끝까지 직선거리는 50m예요. 그런데 만국기를 매단 줄의 길이가 51m밖에 안 되네요! 아무리 생각해도 만국기를 학교 옥상에서 운동장까지 늘어뜨리기엔 줄이 짧은 것 같아요. 비스듬히 멋지게 늘어뜨린 만국기 아래로 청·백군 선수들이 멋지게 입장할 계획이었는데, 어쩌면 좋지요? 그렇다고 건물 옥상이 아니라 낮은 곳에 매단다면 모두들 만국기를 허들처럼 뛰어넘거나 그 아래로 기어가야 할지도 몰라요. 그때 선생님께서 만국기가 달린 줄을 들고 가시더니, 학교 옥상에서 운동장 바닥 끝까지 멋지게 매다셨지 뭐에요? 건물 바닥에서 운동장 끝까지 수평으로 줄을 연결해도 50m가 필요한데, 51m밖에 안 되는 만국기 줄을 가지고 어떻게 10m나 되는 건물 옥상부터 운동장 바닥까지 매달 수 있었을까요? 혹시 선생님이 마법이라도 부린 걸까요?
직각 삼각형의 빗변의 길이를 구하면 돼요
자, 이제 그 비밀을 같이 풀어봅시다. 건물 옥상과 바닥, 그리고 만국기를 연결할 운동장 바닥을 선으로 각각 연결해봐요. 그랬더니 어떤 도형이 생기나요? 그렇죠! 평소에 교과서에서 자주 보던 직각 삼각형이 만들어졌네요.
건물 바닥과 운동장 끝을 연결한 선은 직각 삼각형의 '밑변'이 됐고, 건물 바닥에서 옥상까지는 '높이', 옥상에서 운동장 바닥 끝까지 늘어뜨린 만국기는 '빗변'이 됐어요. 여기서 잠깐! 앞으로 직각 삼각형 하면 바로 떠오르게 될 유명한 수학 공식이 있어요. 고대 그리스의 수학자 피타고라스가 처음으로 증명했다는 이것은 무슨 공식일까요? 바로 직각 삼각형에서 빗변의 제곱은 나머지 두 변의 길이의 제곱의 합과 같다는 '피타고라스의 정리'이지요(제곱은 두 번 곱하는 것을 뜻해요). 그럼 일단 길이의 단위 'm'를 빼고 숫자만으로 계산해봐요.
먼저 밑변에 해당하는 건물에서 운동장까지의 길이 50을 거듭 곱하면 '2500'이 나오죠. 그리고 건물 높이 10을 두번 곱하면 '100'이 나옵니다. 피타고라스 정리에 따르면, 이 둘을 더한 것이 옥상에서 운동장까지 길이를 거듭 곱한 것과 같아야겠지요. 정말 그런지 볼까요? 옥상에서 운동장까지 매달 만국기 길이 51을 두번 곱하니 '2601'이 나왔어요. 우와, 오히려 1m가 남네요. 건물 옥상에서 운동장까지 넉넉히 연결할 수 있겠군요. 이제 선생님이 만국기를 문제 없이 매달 수 있었던 비결을 알겠지요?
토너먼트 방식 경기, 결승전까지 남은 게임 수는?
자자, 만국기 문제를 해결했다고 그냥 가버리면 안 되겠죠? 이번엔 운동회에 숨어 있는 또 다른 수학 이야기를 찾아볼게요.
오늘 운동회 종목 중엔 축구와 농구가 있어요. 축구 경기엔 모두 8개 팀이 참가신청을 했어요. 경기 방식은 토너먼트로 하기로 했고요. '토너먼트'는 경기에서 진 팀은 그 즉시 탈락하고 이긴 팀끼리 다음 경기를 치러 차례로 올라가는 방식이지요. 만약 8개 팀이 토너먼트를 한다면 첫 경기에서 4개 팀이 승리해 남게 되고, 다음 경기엔 2개 팀, 마지막 경기에서 우승팀을 가리는 식이에요.
이렇게 토너먼트 방식으로 대회를 열면 총 몇 번 시합을 해야 할까요? 우선, 8개 팀이 토너먼트를 한다고 하면, 처음에 두 팀씩 맞붙어 경기가 총 4번 펼쳐지겠죠? 그리고 남은 네 팀이 2번 경기를 치르고, 마지막으로 결승전을 벌이겠군요. 그럼 총 7번의 경기가 열리게 되겠군요. 만약 16개 팀이 참가하는 토너먼트라면? 8+4+2+1=15, 이렇게 총 15번 경기가 열리는 것이지요. 32개 팀이 참가하면, 16+8+4+2+1=31이니까 총 31번 경기가 열리고…. 음…, 무언가 법칙이 있다는 느낌이 들지 않나요? 맞아요! 토너먼트 참가팀 수에서 1을 빼면 총 경기 수가 나오는 군요.
홀수 팀이 참가하면 부전승 팀이 생겨요
앗! 그런데 농구 경기는 한 팀이 기권해서 7개 팀만 참가한다고 해요. 두 팀씩 맞붙어 3번 경기를 치르게 되고 나머지 한 팀은 상대가 없어 경기를 하지 않겠네요. 이렇게 경기를 치르지 않고도 다음 단계로 진출하는 것을, 싸우지 않고 이겼다는 뜻에서 '부전승(不戰勝)'이라고 해요. 이런 경우에도 토너먼트 총 경기 수는 전체 참가팀에서 1을 뺀 것과 같을까요? 홀수 팀이 참가했으니 앞에서 살펴본 공식과는 달라져야 하지 않을까요?
참가 팀 수가 홀수일 경우엔 어떤지 계산해봅시다. 7개 팀이 나오면 첫 단계에선 3번 경기가 펼쳐지고 한 팀은 부전승으로 올라갑니다. 이렇게 4개 팀이 가려지면 그 다음엔 두팀씩 맞붙어 각각 경기를 치르고 마지막에 결승 경기가 열리지요. 3+2+1=6, 총 여섯 번 경기가 펼쳐지는군요. 홀수 팀이 참가하든, 부전승 팀이 많든 간에 상관없이 토너먼트 총 경기수는 전체 참가 팀에서 1을 뺀 것과 같다는 공식이 성립한답니다. 그럼 무려 1000개의 팀이 토너먼트에 참가했다 하더라도 총 몇 경기가 펼쳐질지 쉽게 알 수 있겠죠? 1000-1=999, 총 999번 경기가 열린답니다.
삐익! 삐익! 토너먼트 경기 수 계산 방법을 알고는 자신만만해 하고 있는데, 우리 팀이 지고 있다는 소식이 들려오네요. 하지만 아직 운동회의 꽃인 '계주 경기'가 남아 있답니다. 펄럭이는 만국기 아래 힘차게 달려 운동회 우승을 거머쥘 거예요!
[관련교과] 3학년 1학기 '평면도형'
[함께 풀어볼까요]
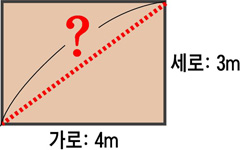
학교 옥상에서 운동장까지 멋지게 만국기를 매단 선생님이 이번에는 운동장에 가로 4m, 세로 3m의 직사각형을 그렸습니다. 그리고 이런 문제를 냈습니다. ‘이 사각형의 두 개의 꼭짓점을 잇는 대각선을 긋는다면 대각선의 길이는 얼마가 될까요?’ 다음 4개의 보기 중에서 고르세요.
① 3m ② 4m ③ 5m ④ 6m
※ '온 가족이 함께 읽는 신문' 조선일보는 지난해 10월25일부터 엄마 아빠가 초등학생 자녀와 함께 읽을 수 있는 교육지면 ‘신문은 선생님’을 만들고 있습니다.
이 지면은 매주 월요일부터 금요일까지 조선일보에 한 페이지씩 실리며 과학, 책 이야기, 창의력 퀴즈, 시사상식,체험학습 등 요일 별로 주제를 달리하고 있습니다. 또 어린이들이 좋아하는 캐릭터를 활용한 ‘둘리 과학여행’, ‘포켓몬 한자왕’과 영어 명작 동화는 고정 코너로 매일 인기리에 연재되고 있습니다.
아이들의 눈높이에 맞춘 친절한 그래픽과 그림, 사진을 활용해서 재미있게 구성한 ‘신문은 선생님’은 매일 정독하면 여러가지 효과를 얻을 수 있습니다. 어려운 과학, 역사가 재미있어 지고 시사 상식이 늘고 사회 이슈가 쉬워집니다. 체험 학습을 어디로 가야할지, 체험학습 보고서는 어떻게 작성할지 이제 고민할 필요가 없습니다.
조선일보

댓글 없음:
댓글 쓰기