2014학년도 경기과학고 2단계 수학
시험에는
① 나열된 원판의 조작 문제
(조합)
② 자연수의 소인수분해와 귀납적 사고를 이용하여 두
수열의 규칙을 찾는 문제 (정수-조합)
③ 유리수의 정수 부분과 소수 부분
(정수)
④ 정사각형으로 둘러싸인 삼각형에서의 합동, 넓이,
평행 등의 활용 (기하)
⑤ 이차함수와 절대값이 있는 함수의 그래프 및 최대, 최소 문제
(대수)
등이 출제되었다. 이번 경기과학고 수학 시험의 가장
큰 특징은 하나의 주제에 대한 다양한 유형의 문제가 혼합 되어 구성된 문항이 많이 늘어났다는 것이다. 구체적으로 말하자면, 1개의
대(大)문항에는 해당 주제에 대한 여러 가지 성질을 추론하고 확인할 수 있는 지를 평가하는 객관식 선다형 소(小) 문항과, 어떤 값을 구하는
문제 해결 과정을 평가하는 단답형 또는 서술형 소(小) 문항이 혼합되어 구성된 경우이다. 특히, 추론 능력을 평가하기 위해 출제된 선다형
소(小) 문항은 학생들 입장에서는 해결 시간이 오래 걸리는 '모두 구하여라'의 형태가 많았다. 이런 문항에 대한 적응력을 키우기 위해서는, 개별
문항 하나 하나를 훈련하는 것 못지않게, 한 주제에 대한 종합적인 학습 또는 스토리 라인 있는 주제 학습이 되도록 해야
한다.
즉, 한 주제에 대해 다양한 실제 예를 계산해 보고,
그 추론을 연역적으로 증명해 보고, 주어진 상황에서 이러한 사실을 바탕으로 해결할 수 있는 문제들을 찾고 해결하는 일련의 학습 과정을 익혀
가야한다.
백화점에서 경품 행사를 하는데 n명의 사람이 지원을 했다.
각각의 사람에게는 1부터 n까지의 번호를 붙인다.
처음에 번호 순서대로 줄을 선 다음, 줄에 있는 사람의 수가 소수이면 맨 앞에 서 있는 사람에게만 선물을 주고 나머지 사람은 번호 순서대로 다시
줄을 선다. 또한 줄에 있는 사람의 수가 합성수이면 사람의 수의 가장 작은 소인수의 배수 번째에 서 있는 사람들에게 선물을 주고 나머지 사람은
다시 번호 순서대로 줄을 선다. 이와 같은 과정을 반복했을때, 마지막에 남은 사람의 번호를 g(n)이라 하고 그 때까지 경품을 나눠 준
횟수를 f(n)이라 하자.
⑴ g(17)+f(17)의 값을
구하여라.
⑵ f(n)에 대하여 다음 중에서 옳은 설명을 모두
골라라.
① f
② f(5³)=2+f(5²)
③ f(2013)=2+f(671)
④ 42명이 참석하였을 때 과정을 2번 진행하면
14명이 남는다.
⑤ 소수 p와 q에 대하여 f(p)=f(q)이면
p=q이다.
⑶ g(n)에 대하여 다음 중에서 옳은 설명을 모두
골라라.
① g(125)=76
② g(1024)=513
③ g(135)=82
④
⑤ a≤b인 두 자연수 a와 b에 대하여
g(a)≤g(b)이다.
|
f(n), g(n)의 규칙을 찾는 것이 쉽지 않은
창의사고 유형 문제이다. 구체적으로 자연수의 소인수분해와 귀납적 사고를 이용하여 두 수열의 규칙을 찾는 문제로서, 귀납적 추론에 대한 충분한
학습이 없다면 거의 노가다식 계산으로 밖에 해결할 수 없다. 아래의 풀이와 같이, 몇 개의 대표 케이스를 통해 점화식을 유추해 보고, 귀납적으로
확인할 수 있도록 해보자.
임의의 소수 p에 대하여 f(p)=1+f(p-1),
g(p)=1+g(p-1)이
성립함을 쉽게 알 수 있다.
좀 더 일반적인 경우의 규칙성을 찾기 위해 예를
들어,
n-135-5²×7 이라 하자.
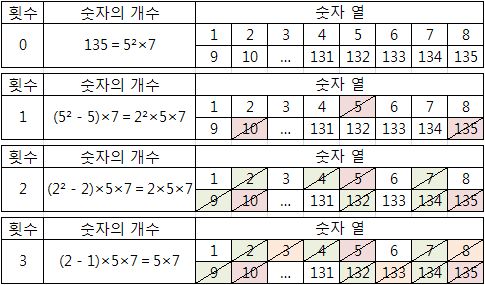
3번 시행한 결과인 숫자 열 1, 6, …, 131은
5×1-4,
5×2-4, …, 5×(5×7)-4로 나타낼 수
있다.
여기서
f(135)=f(35)+3=f(35)+f(5),
1, 2, …, 5×7에 대하여 시행을 시작하는 것과
비교하면,
f(135)=f(35)+3=f(35)+f(5),
g(135)=5g(35)-4=5g(35)-(5-1)임을
추론할 수 있다.
이를 일반화해보면,  ·
· 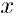 (단,
k≥1)의 가장 작은 소인수가 p일 때,
(단,
k≥1)의 가장 작은 소인수가 p일 때,
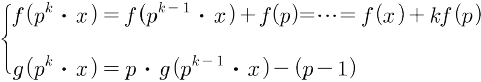
위의 사실들을 이용해 보면, 대부분의 문항들의 답을
계산할 수 있다.
댓글 없음:
댓글 쓰기