2014학년도 서울과학고 2단계 수학
시험에는
① 학급의 자리 배치 방법의 수를 구하는 교란 순열
문제 (조합)
② 점들의 격자가 주어졌을 때, 다양한 삼각형의
개수를 구하는 문제 (조합-기하)
③ 십진법으로 나타낸 자연수의 자릿수 합에 대한 문제
(정수)
④ 구름 모양 사각형에서의 삼각형의 성질을 이용한
증명 문제 (기하)
⑤ 정사면체와 정팔면체를 이용한 분할 문제 (입체
기하)
⑥ 운석 폭발을 소재로 한 융합 문제
등이 출제되었다. 전통적으로 서울과학고 수학 시험은 시간이 부족하고
난이도가 높은 편이다. 특히 전년도까지는 경시형 소재나 문항이 대략 절반까지 출제 된 반면에, 이번 시험의 문항들은 대다수가 문제 해결에
요구되는 지식이 KMO 학습이 꼭 필요한 수준은 아니었다. 시험 자체는 예년에 비해 다소 쉽게 느껴질 수 있으나, 가장 학생들이 선호하는
영재학교인 만큼 다수의 문항을 정확히 해결해야만 안정권일 것으로 보인다.
|
영재반 학생과 창의반 학생은 합동수업을 한다. 영재반
1~16번과 창의반 1~16번이 한 교실에서 수업을 하게 되었는데 영재반 학생들의 자리는 고정되어 있고, 창의반 학생 중 1번과 2번 학생의
자리만 고정되어 있다.
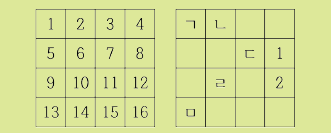
선생님이 수업 도중 칠판에 1, 2, 7, 8,
10, 12, 13을 쓰고 이 번호의 학생들을 일어서게 하였더니 영재반에서 일어난 학생들과 창의반에서 일어난 학생들의 자리가 같았다. 그런데
칠판에 쓴 수들 중에서 몇 개의 수를 지운 뒤에 학생들을 일어서게 하면, 어떤 수를 지우더라도 각 반에서 일어난 학생들의 자리가 완전히 같아지지
않는다는 것을 알았다.
⑴ㄱ, ㄴ, ㄷ, ㄹ, ㅁ에 앉을 수 있는 학생들의
번호의 한 가지 예를 찾으시오.
⑵문제의 조건을 만족하는 ㄱ, ㄴ, ㄷ, ㄹ, ㅁ의
모든 자리 배치의 수를 구하시오.
|
문제의 조건을 해석하여 문제의 결과가 교란순열의
개수를 구하는 것과 같음을 확인하면 어렵지 않게 해결할 수 있는 창의사고 유형문제이다. 해결 방법은 수형도를 이용하거나, 아래의 풀이와 같이
점화식을 이용할 수 있다. 이 교란순열에 대한 학습은 Core-Ⅰ수학 조합 1권 3장에서 접할 수
있다.
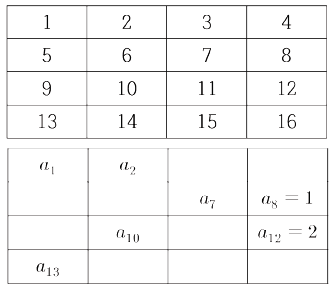
위쪽 표에서 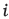 가 있던
위치에 들어갈 수를
가 있던
위치에 들어갈 수를 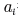 라
하자.
라
하자.
즉, ㄱ, ㄴ, ㄷ, ㄹ, ㅁ에 들어갈 수는
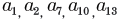 이다.
이다.
(☞ 역으로, 이 조건만 만족하면 문제의 조건을
충족한다.)
이 때 교란순열의 개수 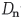 을
이용하여 계산해 보면,
을
이용하여 계산해 보면,

|
사각형 ABCD에서 ∠B+∠C=120˚ 이고
⑴
⑵ 구름모양 사각형 ABCD의 외부에 삼각형 ADE가
정삼각형이 되도록 점 E가 주어져 있을 때, 삼각형 BCE가 정삼각형이다.
|
두 문제 모두 중등 교과 수준의 기하 증명 문제이다.
⑴은 삼각형의 중점연결정리를 이용하여, ⑵는 합동인 두 삼각형을 찾아서 목적 삼각형이 정삼각형임을 보이는 문제이다. 난이도는 높지
않으나, 증명으로 대표되는 연역적 추론 능력을 평가하는 문제이다. 교과 과정의 변화에서 증명에 대한 학습이 축소되었으나, 영재학교를 준비하는
학생이라면 증명 또한 소홀히 하면 안 된다는 것을 보여 주는 단적인 예의 문항이다.
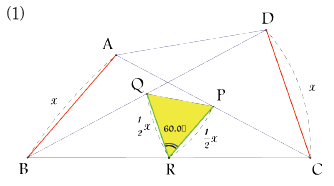
PR//AB이므로
∠PRC=∠ABC
QR//CD이므로
∠QRB=∠DCB
따라서 ∠PRC+∠QRB=120˚
이므로
∠QRP=180˚-∠QRB-∠PRC=60˚
…②
①, ②에 의해 △PQR은
정삼각형이다.
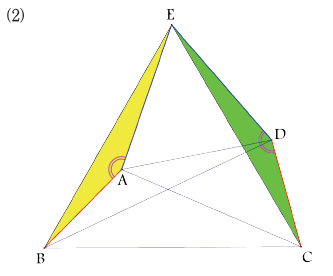
∠DAB=α , ∠CDA=β라 하자.
∠B+∠C=120˚ 이므로 α+β=240˚, 즉
β=240˚-α.
그러면 ∠EAB=360˚-∠EAB-α=300˚-α,
∠EDC=∠EDA+β=60˚+=300˚-α이므로
∠EAB=∠EDC…①
①, ②에 의해 △EDC(SAS 합동)…③
③에 의해
∠AEB=∠DEC이므로
∠BEC=∠AED=60˚…⑤
④, ⑤에 의해 △BCE은
정삼각형이다.
댓글 없음:
댓글 쓰기