2014학년도 영재학교 입시 수학 문항 분석 한국과학영재학교[기출문제]

2014학년도 한국과학영재학교 2단계 수학 시험에는

①입체 도형의 다양한 분할 방법과 공간대각선의 측정법 문제(입체 기하)

②마름모 모양의 문자열에서 다양한 읽기 방법에 따른 경우의 수 문제(조합)

③제시된 지문의 정리와, 눈금 없는 자만을 이용한 작도 문제(기하)

④2차 함수의 그래프에 대한 대수적 해석을 이용해 꼭짓점의 좌표의 근사값을 구하는 문제(대수)

⑤대칭 기준 도형을 이용한 색다른 도형의 변환과 그 때의 점의 자취 문제(기하)

등이 출제되었다. 정답이 여러 개이거나 없는 형태인 개방형 문제의 비중은 전년도에 비해 낮아졌으나, 여전히 문제에 제시된 개념을 바탕으로 하여 사실과 원리를 추론하고, 문제를 해결해 가는 탐구형 문제가 다수를 이루었다. 문항들의 문제 해결에 요구되는 지식은 고등 교과 선행 학습이나 KMO 학습이 꼭 필요한 수준은 아니었으나, 문제 해결에 요구되는 사고력은 심화, 확장할 수 있어야 한다. 즉, 직접적인 선행 학습이라기보다는 다양한 소재와 상황에 대한 심화, 확장 학습이 필요한 문항들이었다.

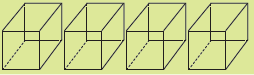
한 변의 길이가 1인 정육면체가 있다. 다음 물음에 답하여라. (1) 주어진 정육면체를 사각뿔 2개와 삼각뿔 2개로 나누려고 한다. 주어진 정육면체에 각각의 입체 도형을 1개씩 따로 그려라. (2) (1)에서 그린 4개의 입체 도형의 겉넓이를 각각 구하고, 그 총합 또한 구하여라. (3) (2)에서 구한 겉넓이의 합과 다른 겉넓이의 합을 갖는 사각뿔 2개와 삼각뿔 2개로 주어진 정육면체를 나누는 방법을 그리고, 겉넓이의 총합을 수하여라. (4) 직육면체 모양의 돌이 있다. 이 돌을 부수지 않고 눈금이 있는 자를 이용하여 공간대각선의 길이를 구하는 대각선의 길이를 자르지 않고, 피타고라스 정리를 사용하지 않고, 구하는 방법을 설명하여라.

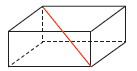(1)~(3)은 중등 교과 수준이며, 정육면체의 다양한 분할 방법과 그 때의 겉넓이의 총합을 묻는 문제이다. 한편 (4)은 학생들에게 익숙한 피타고라스 정리를 이용한 공간대각선의 계산이 아닌, 다른 측정 또는 작도 방법을 이용하여 공간대각선의 길이를 구해 보는 창의적 사고를 묻는 문제이다.

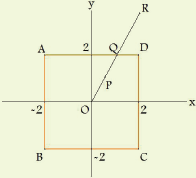
좌표 평면 위에 원점 O와 네 점 A＝(-2,2), B＝(-2,-2), C＝(2,-2), D＝(2,2)가 주어져 있다. 좌표평면 위의 임의의 P점에 대하여 와 사각형 ABCD와의 교점을 Q라 할 때, 을 만족하는 위의 점 R는 유일하게 존재한다. 이 때, 사각형 ABCD를 '대칭 기준 도형'이라 하고, 점 R을 점 P의 사각형 ABCD에 대한 대칭점이라 하자. (1) X=(-1,1), Y(1,1) 에 대하여 점 P가 위를 움직이는 점이라고 하자. 이 때, 점 P의 사각형 ABCD에 대한 대칭점 R의 자취를 구하여라. (2) 점 P가 y＝1위를 움직이는 점이라고 하자. 이 때, 점 P의 사각형 ABCD에 대한 대칭점 R의 자취를 구하여라. (3) 점 P가 y＝1위를 움직이는 점이라고 하자. 점 P의 도형 S에 대한 대칭점 R의 자취가 원이 되는 '대칭 기준 도형' S가 존재하는 지를 보여라.

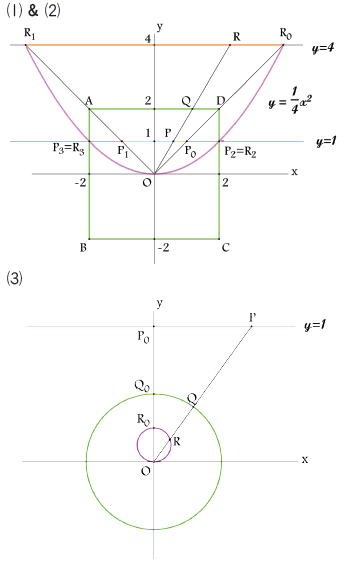
(1)은 삼각형의 닮음을 이용하면 R의 자취가 선분임을 구할 수 있으며, (2)은 P의 좌표를 설정하고, 직접 변환 식을 계산하여 얻은 R의 좌표를 이용하면 자취의 방정식이 2차 함수가 됨을 알 수 있다. (3)은 학생들이 잘 알고 있는 몇 개의 도형을 대칭 기준 도형을 설정하여 시도해 보고, 그러한 결과를 통해 얻은 직관을 활용하여 푸는, 어려운 문제이다. 그런데 이 문제는 Final-345 수학의 6회 8번 반전기하 관련 문제를 풀어본 학생이라면, 바로 결과를 예측할 수 있는 문제이다.

  2014학년도 영재학교 입시 수학 문항 분석 ① - 한국과학영재학교[기출문제