2016년 4월 7일 목요일

음함수(implicit function)와 양함수(explicit function)


수학에서 양함수(explicit function)란, 종속변수 없이 독립변수들의 식만으로 표현되는 함수를 말한다. 독립변수가 하나일 경우, 양함수는 다음과 같은 형태가 된다.
y = f(x)
역으로, 음함수(implicit function)는 종속변수가 독립변수와 분리되지 않은 하나의 관계식으로 주어진 함수를 말한다. 독립변수가 하나일 경우, 음함수는 다음과 같은 형태가 된다.
P(x,y) = 0
음함수를 종속변수에 대해 식을 정리하여 양함수로 만들 수 있는 경우도 있지만, 그렇지 못한 경우도 있다. 이 경우 다가함수(multivalued function)가 된다. 이것은 실질적으로 함수의 정의에서 벗어나므로 함수가 아니지만 함수처럼 취급하면 편리한 경우가 많으므로 통상 '함수'라는 용어를 쓰고 있다.
음함수 정리(the implicit function theorem)는 특정 조건을 만족하는 음함수는 국지적으로 양함수로 바꿀 수 있다는 정리로서, 음함수와 양함수간의 관계를 설명해준다.



양함수와 음함수의 예

몇 가지 예를 통해 음함수와 양함수를 쉽게 이해할 수 있다.

일차함수

다음 함수는 음함수이다.
2x - y - 1 = 0
이 식을 y에 대해 정리하면 양함수가 된다. 즉,
y = 2x - 1
기본적으로 음함수로 표현된 모든 일차함수는 양함수로 표현가능하다.

원의 방정식

다음 식은 원점을 중심으로 하는 반지름이 1인 원을 표현한다.
x^2 + y^2 = 1
이것은 음함수이다. 그러나 하나의 독립변수에 대해 두 개의 종속변수가 할당되므로 이 식은 함수가 아니다. 본질적으로 이 식은 다음 두 개의 양함수를 합친 것이다.
y = \pm\sqrt{1-x^2}
이런 의미에서 일종의 함수로서 취급할 수 있고, 따라서 그 미분도 구할 수 있다.

역함수

주어진 양함수의 역함수를 구하기 위해 독립변수와 종속변수를 바꾸면 즉시 음함수가 된다. 즉,
y = f(x)
이 함수는 양함수이지만, 그 역함수를 구하기 위해 독립변수와 종속변수를 바꾼 다음 식은 음함수가 된다.
x = f(y)
이 식을 양함수로 바꿀 수 있다면 다음과 같이 표현될 것이다.
y = f^{-1}(x)

음함수의 미분

미적분학에서, 음함수의 미분(Implicit differentiation)이란, 연쇄법칙(Chain rule)을 이용한 미분법을 말한다. 음함수를 양함수로 바꾸지 않고 미분한 다음, dy/dx를 계산한다. 이 결과는 양함수로 바꾼 후에 통상적인 미분을 시행한 결과와 같지만 계산이 수월하다는 장점이 있다. 그러나 경우에 따라 양함수로 먼저 바꾸는 쪽이 더 쉬운 경우도 있다.

예 1 : 일차함수

다음과 같은 음함수를 미분하려고 한다.
y + 2x = -4
이를 양함수로 바꾸어 미분하면 다음과 같다.
\frac{dy}{dx} = -2
이번에는 주어진 음함수에 대해 그대로 양변을 미분해보자.
\frac{dy}{dx} + \frac{d(2x)}{dx} = \frac{d(-4)}{dx}
간단한 미적분학의 지식을 통해 다음과 같이 됨을 알 수 있다.
\frac{dy}{dx} + 2 = 0
그리하여 양함수를 미분했을 때와 동일한 결과를 얻게 된다.

예 2 : 원의 방정식

단위원의 방정식이 주어져 있다.
x^2 + y^2 = 1
양변을 미분하여 다음을 얻는다.
2x + 2y\frac{dy}{dx} = 0
y^2을 미분할 때 연쇄법칙(Chain rule)을 이용하였다. 또는 합성함수의 미분이라고 생각해도 좋다. 그래서 정리하면 다음과 같은 결과를 얻는다.
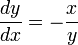
\frac{dy}{dx} = -\frac{x}{y}

위키백과, 

작성자: 시간:

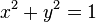
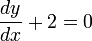
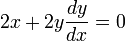
댓글 없음:

댓글 쓰기

피드 구독하기: 댓글 (Atom)