Angle trisection
is a classic problem of compass and straightedge
constructions of ancient Greek mathematics. It concerns construction of an
angle equal to one third of a given arbitrary
angle, using only two tools: an unmarked straightedge, and a compass.
The problem as stated is
generally impossible to solve, as
shown by Pierre Wantzel (1837). Wantzel's proof relies on
ideas from the field of Galois theory—in particular, trisection of an angle
corresponds to the solution of a certain cubic equation, which is not
possible using the given tools. Note that the fact that there is no way to
trisect an angle in general with just a compass and a straightedge does
not mean that there is no trisectible angle: for example, it is
relatively straightforward to trisect a right angle (that is, to construct an angle of
measure 30 degrees).
It is, however, possible
to trisect an arbitrary angle, but using tools other than straightedge and
compass. For example, neusis construction, also known to ancient Greeks,
involves simultaneous sliding and rotation of a marked straightedge, which
cannot be achieved with the original tools. Other techniques were developed by
mathematicians over centuries.
Because it is defined in
simple terms, but complex to prove unsolvable, the problem of angle trisection
is a frequent subject of pseudomathematical attempts at solution by naive
enthusiasts. The "solutions" often involve mistaken interpretations of the
rules, or are simply incorrect.[1]
Angles may be trisected via a Neusis
construction, but this uses tools outside the Greek
framework of an unmarked straightedge and a compass.
Note that cos(60°) .
Then by the triple-angle formula,
.
Then by the triple-angle formula,  and so
and so  .
Thus
.
Thus  ,
or equivalently
,
or equivalently  .
Now substitute
.
Now substitute  ,
so that
,
so that  .
Let
.
Let  .
.
The general problem of angle trisection is solvable, but using additional
tools, and thus going outside of the original Greek framework of compass and
straightedge.
This requires three facts from geometry (at right):
Hutcheson constructed a cylinder from the angle to be trisected by drawing an
arc across the angle, completing it as a circle, and constructing from that
circle a cylinder on which a, say, equilateral triangle was inscribed (a
360-degree angle divided in three). This was then "mapped" onto the angle to be
trisected, with a simple proof of similar triangles.
Note that while a tomahawk is constructible with compass and straightedge, it
is not generally possible to construct a tomahawk in any desired position. Thus,
the above construction does not contradict the nontrisectibility of angles with
ruler and compass alone.
Background and problem statement[edit]
Using only an unmarked
straightedge and a compass, Greek mathematicians found means to divide a line into an arbitrary set of equal segments, to
draw parallel lines, to bisect angles, to construct
many polygons, and to construct
squares of equal or twice the area of a given
polygon.
Three problems proved
elusive, specifically, trisecting the angle, doubling the cube, and squaring the circle. The problem of angle
trisection reads:
Construct an angle equal to one-third of a given arbitrary angle
(or divide it into three equal angles), using only two tools:
- an un-marked straightedge and
- a compass.
Proof of impossibility[edit]
The problem of
constructing an angle of a given measure  is equivalent to constructing two segments such that the ratio of their length
is
is equivalent to constructing two segments such that the ratio of their length
is  because one may pass from one solution to the other by a compass and
straightedge construction. It follows that, given a segment that is sought as
having a unit length, the problem of angle trisection is equivalent to
constructing a segment whose length is the root of a cubic polynomial — since by
the triple-angle formula,
because one may pass from one solution to the other by a compass and
straightedge construction. It follows that, given a segment that is sought as
having a unit length, the problem of angle trisection is equivalent to
constructing a segment whose length is the root of a cubic polynomial — since by
the triple-angle formula,  This allows to reduce the original geometric problem to a purely algebraic
problem.
This allows to reduce the original geometric problem to a purely algebraic
problem.
 is equivalent to constructing two segments such that the ratio of their length
is
is equivalent to constructing two segments such that the ratio of their length
is  because one may pass from one solution to the other by a compass and
straightedge construction. It follows that, given a segment that is sought as
having a unit length, the problem of angle trisection is equivalent to
constructing a segment whose length is the root of a cubic polynomial — since by
the triple-angle formula,
because one may pass from one solution to the other by a compass and
straightedge construction. It follows that, given a segment that is sought as
having a unit length, the problem of angle trisection is equivalent to
constructing a segment whose length is the root of a cubic polynomial — since by
the triple-angle formula,  This allows to reduce the original geometric problem to a purely algebraic
problem.
This allows to reduce the original geometric problem to a purely algebraic
problem.
One can show that every
rational number is constructible and that every irrational number which is constructible in one step from some given numbers
is a root of a polynomial of degree 2 with coefficients in the field generated by these numbers. Therefore any
number which is constructible by a series of steps is a root of a minimal polynomial whose
degree is a power of 2. Note also that 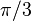 radians (60 degrees, written 60°) is constructible. We now show that it is impossible to
construct a 20° angle; this implies that a 60° angle cannot be trisected, and
thus that an arbitrary angle cannot be trisected.
radians (60 degrees, written 60°) is constructible. We now show that it is impossible to
construct a 20° angle; this implies that a 60° angle cannot be trisected, and
thus that an arbitrary angle cannot be trisected.
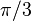 radians (60 degrees, written 60°) is constructible. We now show that it is impossible to
construct a 20° angle; this implies that a 60° angle cannot be trisected, and
thus that an arbitrary angle cannot be trisected.
radians (60 degrees, written 60°) is constructible. We now show that it is impossible to
construct a 20° angle; this implies that a 60° angle cannot be trisected, and
thus that an arbitrary angle cannot be trisected.
Denote the set of rational numbers by Q. If 60° could be
trisected, the degree of a minimal polynomial of cos(20°) over Q would be a power of two. Now let
y = cos(20°).
 .
Then by the triple-angle formula,
.
Then by the triple-angle formula,  and so
and so  .
Thus
.
Thus  ,
or equivalently
,
or equivalently  .
Now substitute
.
Now substitute  ,
so that
,
so that  .
Let
.
Let  .
.
The minimal polynomial
for x (hence cos(20°)) is a factor of 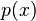 .
Because
.
Because 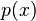 is degree 3, if it is reducible over by Q then it has a rational root. By the rational root theorem, this root must be 1 or −1,
but both are clearly not roots. Therefore
is degree 3, if it is reducible over by Q then it has a rational root. By the rational root theorem, this root must be 1 or −1,
but both are clearly not roots. Therefore 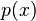 is irreducible over by
Q, and the minimal polynomial for cos(20°) is
of degree 3.
is irreducible over by
Q, and the minimal polynomial for cos(20°) is
of degree 3.
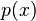 .
Because
.
Because 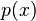 is degree 3, if it is reducible over by Q then it has a rational root. By the rational root theorem, this root must be 1 or −1,
but both are clearly not roots. Therefore
is degree 3, if it is reducible over by Q then it has a rational root. By the rational root theorem, this root must be 1 or −1,
but both are clearly not roots. Therefore 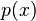 is irreducible over by
Q, and the minimal polynomial for cos(20°) is
of degree 3.
is irreducible over by
Q, and the minimal polynomial for cos(20°) is
of degree 3.
So an angle of 60° =
(1/3)π radians cannot be
trisected.
Many people (who
presumably are unaware of the above result, misunderstand it, or incorrectly
reject it) have proposed methods of trisecting the general angle. Some of these
methods provide reasonable approximations; others (some of which are mentioned
below) involve tools not permitted in the classical problem. The mathematician
Underwood Dudley has
detailed some of these failed attempts in his book The Trisectors.[2]
Angles which can be trisected[edit]
However, some angles can
be trisected. For example, for any angle  ,
the angle
,
the angle 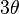 can be trivially trisected by ignoring the given angle and directly constructing
an angle of measure
can be trivially trisected by ignoring the given angle and directly constructing
an angle of measure  .
There are angles which are not constructible, but are trisectible. For example,
.
There are angles which are not constructible, but are trisectible. For example,
 is such an angle: five copies of
is such an angle: five copies of  combine to make an angle of measure
combine to make an angle of measure  ,
which is a full circle plus the desired
,
which is a full circle plus the desired  .
More generally, for a positive integer
.
More generally, for a positive integer  ,
an angle of measure
,
an angle of measure 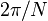 is trisectible if and only if
is trisectible if and only if  does not divide
does not divide  ;[3] if
;[3] if  is a prime number, this angle is
constructible if and only if
is a prime number, this angle is
constructible if and only if  is a Fermat prime.
is a Fermat prime.
 ,
the angle
,
the angle 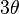 can be trivially trisected by ignoring the given angle and directly constructing
an angle of measure
can be trivially trisected by ignoring the given angle and directly constructing
an angle of measure  .
There are angles which are not constructible, but are trisectible. For example,
.
There are angles which are not constructible, but are trisectible. For example,
 is such an angle: five copies of
is such an angle: five copies of  combine to make an angle of measure
combine to make an angle of measure  ,
which is a full circle plus the desired
,
which is a full circle plus the desired  .
More generally, for a positive integer
.
More generally, for a positive integer  ,
an angle of measure
,
an angle of measure 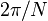 is trisectible if and only if
is trisectible if and only if  does not divide
does not divide  ;[3] if
;[3] if  is a prime number, this angle is
constructible if and only if
is a prime number, this angle is
constructible if and only if  is a Fermat prime.
is a Fermat prime.One general theorem[edit]
Again, denote the rational numbers as Q:
The proof is a relatively straightforward
generalization of the proof given above that a 60-degree angle is not
trisectible.[4]
Trisection using other methods[edit]
By infinite repetition of bisection[edit]
Trisection can be
achieved by infinite repetition of the compass and straightedge method for
bisecting an angle. The geometric series 1/3 = 1/4+1/16+1/64+1/256+... or 1/3 =
1/2-1/4+1/8-1/16+... can be used as a basis for the bisections. This method is
considered to be breaking the rules for compass and straightedge construction as
it involves an infinite number of steps. However, an approximation to any degree
of accuracy can be obtained in a finite number of steps.[5]
Using origami[edit]
Main article: Mathematics of origami#Trisecting an
angle
Trisection, like many
constructions impossible by ruler and compass, can easily be accomplished by the
more powerful operations of paper folding, or origami. Huzita's axioms (types of
folding operations) can construct cubic extensions (cube roots) of given
lengths, whereas ruler-and-compass can construct only quadratic extensions
(square roots).
With an auxiliary curve[edit]
There are certain
curves called trisectrices which, if drawn
on the plane using other methods, can be used to trisect arbitrary angles.[6]
With a marked ruler[edit]
Another means to
trisect an arbitrary angle by a "small" step outside the Greek framework is via
a ruler with two marks a set distance apart. The next construction is originally
due to Archimedes, called a Neusis construction, i.e., that uses tools
other than an un-marked straightedge. The diagrams we use show this
construction for an acute angle, but it indeed works for any angle up to 180
degrees.
- Any full set of angles on a straight line add to 180°,
- The sum of angles of any triangle is 180°, and,
- Any two equal sides of an isosceles triangle will meet the third in the same angle.
Let l be the
horizontal line in the diagram on the right. Angle a (left of point
B) is the subject of trisection. First, a point A is drawn at an
angle's ray, one unit apart from B. A circle of radius AB is drawn. Then, the markedness of
the ruler comes into play: one mark of the ruler is placed at A and the
other at B. While keeping the ruler (but not the mark) touching A,
the ruler is slid and rotated until one mark is on the circle and the other is
on the line l. The mark on the circle is labeled C and the mark on
the line is labeled D. This ensures that CD = AB. A radius
BC is drawn to make it obvious that line segments AB, BC,
and CD all have equal length. Now, Triangles ABC and BCD
are isosceles, thus (by Fact 3 above) each has two
equal angles.
Hypothesis: Given AD is a straight line, and
AB, BC, and CD are all equal length,
Conclusion: angle  .
.
 .
.- From Fact 1) above,
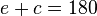 °.
°.
- Looking at triangle BCD, from Fact 2)
 °.
°.
- From the last two equations,
 .
.
- From Fact 2),
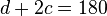 °,
thus
°,
thus 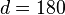 °
°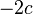 ,
so from last,
,
so from last, 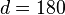 °
°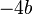 .
.
- From Fact 1) above,
 °,
thus
°,
thus 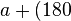 °
° °.
°.
Again, this
construction stepped outside the framework of allowed constructions by
using a marked straightedge.
With a string[edit]
Thomas Hutcheson
published an article in the Mathematics Teacher[7] that used a
string instead of a compass and straight edge. A string can be used as either a
straight edge (by stretching it) or a compass (by fixing one point and
identifying another), but can also wrap around a cylinder, the key to
Hutcheson's solution.
With a "tomahawk"[edit]
A "tomahawk" is a geometric
shape consisting of a semicircle and two orthogonal line segments, such that the
length of the shorter segment is equal to the circle radius. Trisection is
executed by leaning the end of the tomahawk's shorter segment on one ray, the
circle's edge on the other, so that the "handle" (longer segment) crosses the
angle's vertex; the trisection line runs between the vertex and the center of
the semicircle.
The tomahawk produces
the same geometric effect as the paper-folding method: the distance between
circle center and the tip of the shorter segment is twice the distance of the
radius, which is guaranteed to contact the angle. It is also equivalent to the
use of an architects L-Ruler ( Carpenter's Square).
With interconnected compasses[edit]
An angle can be
trisected with a device that is essentially a four-pronged version of a compass,
with linkages between the prongs designed to keep the three angles between
adjacent prongs equal.[8]
Wikipedia




 is reducible over the
is reducible over the  .
.

 ,
or
,
or  ,
and the
,
and the 
댓글 없음:
댓글 쓰기