녹원학원 수학과학영재교육 010-3549-5206 : Mathematical proof

In mathematics, a proof is a deductive argument for a mathematical statement. In the argument, other previously established statements, such as theorems, can be used. In principle, a proof can be traced back to generally accepted statements, known as axioms.^[1]^[2] Proofs are examples of deductive reasoning and are distinguished from inductive or empirical arguments; a proof must demonstrate that a statement is always true (occasionally by listing all possible cases and showing that it holds in each), rather than enumerate many confirmatory cases. An unproven statement that is believed true is known as a conjecture.

Proofs employ logic but usually include some amount of natural language which usually admits some ambiguity. In fact, the vast majority of proofs in written mathematics can be considered as applications of rigorous informal logic. Purely formal proofs, written in symbolic language instead of natural language, are considered in proof theory. The distinction between formal and informal proofs has led to much examination of current and historical mathematical practice, quasi-empiricism in mathematics, and so-called folk mathematics (in both senses of that term). The philosophy of mathematics is concerned with the role of language and logic in proofs, and mathematics as a language.

History and etymology[edit]

Nature and purpose[edit]

As practised, a proof is expressed in natural language and is a rigorous argument intended to convince the audience of the truth of a statement. The standard of rigor is not absolute and has varied throughout history. A proof can be presented differently depending on the intended audience. In order to gain acceptance, a proof has to meet communal statements of rigor; an argument considered vague or incomplete may be rejected.

The concept of a proof is formalized in the field of mathematical logic.^[10] A formal proof is written in a formal language instead of a natural language. A formal proof is defined as sequence for formulas in a formal language in which each formula is a logical consequence of preceding formulas. Having a definition of formal proof makes the concept of proof amenable to study. Indeed, the field of proof theory studies formal proofs and their properties, for example, the property that a statement has a formal proof. An application of proof theory is to show that certain undecidable statements are not provable.

The definition of a formal proof is intended to capture the concept of proofs as written in the practice of mathematics. The soundness of this definition amounts to the belief that a published proof can, in principle, be converted into a formal proof. However, outside the field of automated proof assistants, this is rarely done in practice. A classic question in philosophy asks whether mathematical proofs are analytic or synthetic. Kant, who introduced the analytic-synthetic distinction, believed mathematical proofs are synthetic.

Proofs may be viewed as aesthetic objects, admired for their mathematical beauty. The mathematician Paul Erdős was known for describing proofs he found particularly elegant as coming from "The Book", a hypothetical tome containing the most beautiful method(s) of proving each theorem. The book Proofs from THE BOOK, published in 2003, is devoted to presenting 32 proofs its editors find particularly pleasing.

Methods of proof[edit]

Direct proof[edit]

Main article: Direct proof

In direct proof, the conclusion is established by logically combining the axioms, definitions, and earlier theorems.^[11] For example, direct proof can be used to establish that the sum of two even integers is always even:

Consider two even integers x and y. Since they are even, they can be written as x = 2a and y = 2b, respectively, for integers a and b. Then the sum x + y = 2a + 2b = 2(a+b). Therefore x+y has 2 as a factor and, by definition, is even. Hence the sum of any two even integers is even.

This proof uses the definition of even integers, the integer properties of closure under addition and multiplication, and distributivity.

Proof by mathematical induction[edit]

Main article: Mathematical induction

Mathematical induction is not a form of inductive reasoning. In proof by mathematical induction, a single "base case" is proved, and an "induction rule" is proved, which establishes that a certain case implies the next case. Applying the induction rule repeatedly, starting from the independently proved base case, proves many, often infinitely many, other cases.^[12] Since the base case is true, the infinity of other cases must also be true, even if all of them cannot be proved directly because of their infinite number. A subset of induction is infinite descent. Infinite descent can be used to prove the irrationality of the square root of two.

A common application of proof by mathematical induction is to prove that a property known to hold for one number holds for all natural numbers:^[13] Let

N = {1,2,3,4,...

} be the set of natural numbers, and

P (n)

be a mathematical statement involving the natural number

n

belonging to

N

such that

(ii)

P (n +1)

is true whenever

P (n)

is true, i.e.,

P (n)

is true implies that

P (n +1)

is true.

Then $P (n)$ is true for all natural numbers $n$ .

For example, we can prove by induction that all integers of the form

2 n + 1

are odd:

(i) For

n = 1

2 n + 1 = 2(1) + 1 = 3

, and

3

is odd. Thus

P (1)

is true.

(ii) For

2 n + 1

for some

n

2(n +1) + 1 = (2 n +1) + 2

. If

2 n + 1

is odd, then

(2 n +1) + 2

must also be odd, because adding

2

to an odd number results in an odd number. So

P (n +1)

is true if

P (n)

is true.

Thus

2 n + 1

is odd, for all natural numbers

n

It is common for the phrase "proof by induction" to be used for a "proof by mathematical induction".^[14]

Proof by contraposition[edit]

Main article: Contraposition

Proof by contraposition infers the conclusion "if p then q" from the premise "if not q then not p". The statement "if not q then not p" is called the contrapositive of the statement "if p then q". For example, contraposition can be used to establish that, given an integer x, if x² is even, then x is even:

Suppose x is not even. Then x is odd. The product of two odd numbers is odd, hence x² = x·x is odd. Thus x² is not even.

Proof by contradiction[edit]

Main article: Proof by contradiction

In proof by contradiction (also known as reductio ad absurdum, Latin for "by reduction to the absurd"), it is shown that if some statement were true, a logical contradiction occurs, hence the statement must be false. A famous example of proof by contradiction shows that $\sqrt{2}$ is an irrational number:

Suppose that $\sqrt{2}$ were a rational number, so by definition $\sqrt{2} = {a\over b}$ where a and b are non-zero integers with no common factor. Thus, $b\sqrt{2} = a$ . Squaring both sides yields 2b² = a². Since 2 divides the left hand side, 2 must also divide the right hand side (as they are equal and both integers). So a² is even, which implies that a must also be even. So we can write a = 2c, where c is also an integer. Substitution into the original equation yields 2b² = (2c)² = 4c². Dividing both sides by 2 yields b² = 2c². But then, by the same argument as before, 2 divides b², so b must be even. However, if a and b are both even, they share a factor, namely 2. This contradicts our assumption, so we are forced to conclude that $\sqrt{2}$ is an irrational number.

Proof by construction[edit]

Main article: Proof by construction

Proof by construction, or proof by example, is the construction of a concrete example with a property to show that something having that property exists. Joseph Liouville, for instance, proved the existence of transcendental numbers by constructing an explicit example. It can also be used to construct a counterexample to disprove a proposition that all elements have a certain property.

Proof by exhaustion[edit]

Main article: Proof by exhaustion

In proof by exhaustion, the conclusion is established by dividing it into a finite number of cases and proving each one separately. The number of cases sometimes can become very large. For example, the first proof of the four color theorem was a proof by exhaustion with 1,936 cases. This proof was controversial because the majority of the cases were checked by a computer program, not by hand. The shortest known proof of the four color theorem as of 2011 still has over 600 cases.

Probabilistic proof[edit]

Main article: Probabilistic method

A probabilistic proof is one in which an example is shown to exist, with certainty, by using methods of probability theory. Probabilistic proof, like proof by construction, is one of many ways to show existence theorems.

This is not to be confused with an argument that a theorem is 'probably' true, a 'plausibility argument'. The work on the Collatz conjecture shows how far plausibility is from genuine proof.^[15]

Combinatorial proof[edit]

Main article: Combinatorial proof

A combinatorial proof establishes the equivalence of different expressions by showing that they count the same object in different ways. Often a bijection between two sets is used to show that the expressions for their two sizes are equal. Alternatively, a double counting argument provides two different expressions for the size of a single set, again showing that the two expressions are equal.

Nonconstructive proof[edit]

Main article: Nonconstructive proof

A nonconstructive proof establishes that a mathematical object with a certain property exists without explaining how such an object can be found. Often, this takes the form of a proof by contradiction in which the nonexistence of the object is proven to be impossible. In contrast, a constructive proof establishes that a particular object exists by providing a method of finding it. A famous example of a nonconstructive proof shows that there exist two irrational numbers a and b such that $a^b$ is a rational number:

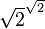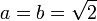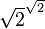Either $\sqrt{2}^{\sqrt{2}}$ is a rational number and we are done (take $a=b=\sqrt{2}$ ), or $\sqrt{2}^{\sqrt{2}}$ is irrational so we can write $a=\sqrt{2}^{\sqrt{2}}$ and $b=\sqrt{2}$ . This then gives $\left (\sqrt{2}^{\sqrt{2}}\right )^{\sqrt{2}}=\sqrt{2}^{2}=2$ , which is thus a rational of the form $a^b.$

Statistical proofs in pure mathematics[edit]

Main article: Statistical proof

The expression "statistical proof" may be used technically or colloquially in areas of pure mathematics, such as involving cryptography, chaotic series, and probabilistic or analytic number theory.^[16]^[17]^[18] It is less commonly used to refer to a mathematical proof in the branch of mathematics known as mathematical statistics. See also "Statistical proof using data" section below.

Computer-assisted proofs[edit]

Main article: Computer-assisted proof

Until the twentieth century it was assumed that any proof could, in principle, be checked by a competent mathematician to confirm its validity.^[5] However, computers are now used both to prove theorems and to carry out calculations that are too long for any human or team of humans to check; the first proof of the four color theorem is an example of a computer-assisted proof. Some mathematicians are concerned that the possibility of an error in a computer program or a run-time error in its calculations calls the validity of such computer-assisted proofs into question. In practice, the chances of an error invalidating a computer-assisted proof can be reduced by incorporating redundancy and self-checks into calculations, and by developing multiple independent approaches and programs. Errors can never be completely ruled out in case of verification of a proof by humans either, especially if the proof contains natural language and requires deep mathematical insight.

Undecidable statements[edit]

(i) P(1) is true, i.e., P(n) is true for n = 1.
A statement that is neither provable nor disprovable from a set of axioms is called undecidable (from those axioms). One example is the parallel postulate, which is neither provable nor refutable from the remaining axioms of Euclidean geometry.

Mathematicians have shown there are many statements that are neither provable nor disprovable in Zermelo-Fraenkel set theory with the axiom of choice (ZFC), the standard system of set theory in mathematics (assuming that ZFC is consistent); see list of statements undecidable in ZFC.

Gödel's (first) incompleteness theorem shows that many axiom systems of mathematical interest will have undecidable statements.

Heuristic mathematics and experimental mathematics[edit]

Main article: Experimental mathematics

While early mathematicians such as Eudoxus of Cnidus did not use proofs, from Euclid to the foundational mathematics developments of the late 19th and 20th centuries, proofs were an essential part of mathematics.^[19] With the increase in computing power in the 1960s, significant work began to be done investigating mathematical objects outside of the proof-theorem framework,^[20] in experimental mathematics. Early pioneers of these methods intended the work ultimately to be embedded in a classical proof-theorem framework, e.g. the early development of fractal geometry,^[21] which was ultimately so embedded.

Related concepts[edit]

Visual proof[edit]

Although not a formal proof, a visual demonstration of a mathematical theorem is sometimes called a "proof without words". The left-hand picture below is an example of a historic visual proof of the Pythagorean theorem in the case of the (3,4,5) triangle.
- Visual proof for the (3, 4, 5) triangle as in the Chou Pei Suan Ching 500–200 BC.
- Animated visual proof for the Pythagorean theorem by rearrangement.
- A second animated proof of the Pythagorean theorem.
Elementary proof[edit]

Main article: Elementary proof

An elementary proof is a proof which only uses basic techniques. More specifically, the term is used in number theory to refer to proofs that make no use of complex analysis. For some time it was thought that certain theorems, like the prime number theorem, could only be proved using "higher" mathematics. However, over time, many of these results have been reproved using only elementary techniques.

Two-column proof[edit]

A two-column proof published in 1913
A particular way of organising a proof using two parallel columns is often used in elementary geometry classes in the United States.^[22] The proof is written as a series of lines in two columns. In each line, the left-hand column contains a proposition, while the right-hand column contains a brief explanation of how the corresponding proposition in the left-hand column is either an axiom, a hypothesis, or can be logically derived from previous propositions. The left-hand column is typically headed "Statements" and the right-hand column is typically headed "Reasons".^[23]

Colloquial use of "mathematical proof"[edit]

The expression "mathematical proof" is used by lay people to refer to using mathematical methods or arguing with mathematical objects, such as numbers, to demonstrate something about everyday life, or when data used in an argument is numerical. It is sometimes also used to mean a "statistical proof" (below), especially when used to argue from data.

Statistical proof using data[edit]

Main article: Statistical proof

"Statistical proof" from data refers to the application of statistics, data analysis, or Bayesian analysis to infer propositions regarding the probability of data. While using mathematical proof to establish theorems in statistics, it is usually not a mathematical proof in that the assumptions from which probability statements are derived require empirical evidence from outside mathematics to verify. In physics, in addition to statistical methods, "statistical proof" can refer to the specialized mathematical methods of physics applied to analyze data in a particle physics experiment or observational study in cosmology. "Statistical proof" may also refer to raw data or a convincing diagram involving data, such as scatter plots, when the data or diagram is adequately convincing without further analysis.

Inductive logic proofs and Bayesian analysis[edit]

Main articles: Inductive logic and Bayesian analysis

Proofs using inductive logic, while considered mathematical in nature, seek to establish propositions with a degree of certainty, which acts in a similar manner to probability, and may be less than one certainty. Bayesian analysis establishes assertions as to the degree of a person's subjective belief. Inductive logic should not be confused with mathematical induction.

Proofs as mental objects[edit]

Main articles: Psychologism and Language of thought

Psychologism views mathematical proofs as psychological or mental objects. Mathematician philosophers, such as Leibniz, Frege, and Carnap, have attempted to develop a semantics for what they considered to be the language of thought, whereby standards of mathematical proof might be applied to empirical science.

Influence of mathematical proof methods outside mathematics[edit]

Philosopher-mathematicians such as Spinoza have attempted to formulate philosophical arguments in an axiomatic manner, whereby mathematical proof standards could be applied to argumentation in general philosophy. Other mathematician-philosophers have tried to use standards of mathematical proof and reason, without empiricism, to arrive at statements outside of mathematics, but having the certainty of propositions deduced in a mathematical proof, such as Descarte's cogito argument.

Ending a proof[edit]

Main article: Q.E.D.

Sometimes, the abbreviation "Q.E.D." is written to indicate the end of a proof. This abbreviation stands for "Quod Erat Demonstrandum", which is Latin for "that which was to be demonstrated". A more common alternative is to use a square or a rectangle, such as □ or ∎, known as a "tombstone" or "halmos" after its eponym Paul Halmos. Often, "which was to be shown" is verbally stated when writing "QED", "□", or "∎" in an oral presentation on a board.

Wikipedia

녹원학원 수학과학영재교육 010-3549-5206

2013년 10월 25일 금요일

Mathematical proof

History and etymology[edit]

Nature and purpose[edit]

Methods of proof[edit]

Direct proof[edit]

Proof by mathematical induction[edit]

Proof by contraposition[edit]

Proof by contradiction[edit]

Proof by construction[edit]

Proof by exhaustion[edit]

Probabilistic proof[edit]

Combinatorial proof[edit]

Nonconstructive proof[edit]

Statistical proofs in pure mathematics[edit]

Computer-assisted proofs[edit]

Undecidable statements[edit]

Heuristic mathematics and experimental mathematics[edit]

Related concepts[edit]

Visual proof[edit]

Elementary proof[edit]

Two-column proof[edit]

Colloquial use of "mathematical proof"[edit]

Statistical proof using data[edit]

Inductive logic proofs and Bayesian analysis[edit]

Proofs as mental objects[edit]

Influence of mathematical proof methods outside mathematics[edit]

Ending a proof[edit]

댓글 없음: