작도는 눈금 없는 자와 컴퍼스만을 이용해 여러가지 도형을 그리는 고전 기하학의 여러 가지 문제들을 가리킨다. 이때 자는
직선을 긋는 용도로만 사용되고, 컴퍼스는 원을
그리고, 선분의 길이를 옮기는 데에 사용된다.
정다각형의 작도
정다각형을 작도하다보면 작도가 될때도 있고 안될때도 있다. 이런 사실은 '어떤 정다각형은 작도가 가능하고 어떤 정다각형이 작도가 불가능하냐'로 이어졌다. 작도 가능한 정다각형의 판정방법은 다음과 같다.
- 만약
 이
2의 거듭제곱과 서로 다른 페르마 소수의 곱들로 이루어져 있을 때, 정
이
2의 거듭제곱과 서로 다른 페르마 소수의 곱들로 이루어져 있을 때, 정 각형은
작도 가능하다.
각형은
작도 가능하다.
즉 다시말해서, 정다각형의 작도 가능공식은 다음과 같다.
 이
페르마 수일 경우, 즉
이
페르마 수일 경우, 즉 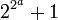 의
꼴의 수 중에서 소수라면 작도 가능하다.
의
꼴의 수 중에서 소수라면 작도 가능하다.
 이
서로 다른 페르마 소수들의 곱일 경우 작도 가능하다.
이
서로 다른 페르마 소수들의 곱일 경우 작도 가능하다.
- 정
 각형이
가능할 경우 정
각형이
가능할 경우 정 각형도
가능하다.
각형도
가능하다.
기본적인 작도[편집]
아래 작도들은 중학교 1학년 수준이다.
각의 이등분선[편집]
- 점 O를 중심으로 하는 적당한 크기의 원을 그려 반직선 OX, 반직선 OY와의 교점을 각각 A, B라고 한다.
- 점 A, B를 중심으로 하고 반지름 길이가 같은 두 원을 그려, 그 교점을 P라고 한다.
- 반직선 OP를 그린다.
증명[편집]
선분 OA=선분 OB, 선분 AP=선분 BP,
선분 OP는 공통 (SSS합동) 각 AOP와 각 BOP가 서로 대응각이므로
선분 OP는 각의 이등분선이다.
선분의 수직이등분선[편집]
- 선분의 양 끝점을 중심으로, 반지름이 선분의 반보다 적당히 큰 원을 둘 그린다.
- 두 원이 만나서 생기는 교점끼리 잇는다.
증명[편집]
위와 같이 해서 마름모를 그릴 수 있다. 마름모의 대각선의 성질은 서로 수직 이등분한다는것이다. 따라서, 수직이등분하려는 위의 선분은 수직이등분된다. 또한, 마름모의 네 변의 길이는 모두 같으므로 작도 과정에서 생긴 두 원의 교점을 각각 P, Q라고 하고 선분의 양 끝점을 각각 A, B라고 할 때 점 A, B에서 점 P, Q와의 거리는 모두 같다.
- 점 O를 중심으로 하는 적당한 크기의 원을 그려 반직선 OX, 반직선 OY와의 교점을 각각 A, B라고 한다.
- 컴퍼스 크기를 그대로 하여 점 P를 중심으로 하는 원을 그려 반직선 PQ와의 교점을 D라고 한다.
- 점 D를 중심으로 하고 선분 AB를 반지름으로 하는 원을 그려 위 원과의 교점을 C라고 한다.
수선 (평각의 이등분)[편집]
- 점 P를 중심으로 적당한 크기의 원을 그려서 직선 l과 만나는 교점을 각각 A, B라고 한다. (점P는 직선l위에 있지 않다.)
- 점 A를 중심으로 적당한 원을 그린다.
- 점 B를 중심으로 반지름 길이가 위와 같은 원을 그린다. 그리고 위 원과의 교점을 Q라고 한다.
- 직선 PQ를 그린다.
선분의 등분[편집]
- 등분하고자 하는 선분에서 임의의 각도로 반직선을 하나 긋는다.
- 반직선의 시작점에서 일정한 길이씩 떨어진
 개의
점을 만든다.
개의
점을 만든다.
- 가장 끝의 점과 선분의 반직선과 접하지 않은 끝을 잇는다.
- 3번의 선분과 평행하고 두 번째 점과 접하는 직선을 그린다.
- 점이 끝날때까지 평행한 선을 계속 그린다.
정삼각형[편집]
- 선분의 양 끝 점에서 반지름이 선분과 같은 두 원을 그린다.
- 이때 생기는 교점과 선분 양 끝점을 잇는다.
평행선[편집]
- 점 P를 지나면서 직선 l과 만나는 직선을 그어 그 교점을 점 A라고 한다.
- 점 A를 중심으로 적당한 크기의 원을 그려 직선 PA, 직선 l과의 교점을 각각 B, C라고 한다.
- 점 P를 중심으로 반지름의 길이가 위와 같은 원을 그려 직선 PA와의 교점을 점 Q라고 한다.
- 점 B를 중심으로 반지름의 길이가 선분 BC와 같은 원을 그린다.
- 점 Q를 중심으로 반지름의 길이가 4. 와 같은 원을 그려 3. 원과의 교점을 점 R이라고 한다.
- 직선 PR을 그린다.
직각의 3등분[편집]
임의의 각을 3등분 하는 작도는 '3대 작도 불가능 문제' 중 하나지만, 정삼각형을 이용하면 30도를 작도할 수 있으므로 직각은 3등분할 수 있다. 직각의 삼등분 순서는 다음과 같다.
- 직각에서 임의의 반지름을 가지는 호 AB를 그린다. (이하 호의 중심은 O)
- A를 중심으로 1과 같은 반지름을 가지는 호 OD 를 그린다. (이때 D는 호 AB와 원 A 의 교점)
- B를 중심으로 1과 같은 반지름을 가지는 호 OE 를 그린다. (이때 E는 호 AB와 원 B 의 교점)
- O 와 D,E 를 이으면 직각이 삼등분된것이다.
자 없이 컴퍼스만으로 하는 작도[편집]
3대 작도 불가능 문제[편집]
3대 작도 불가능
문제(3大作圖不可能問題)는 고대 그리스 시대부터 내려온 세 가지 작도
문제이다. 2000년 이상의 오랜 시간 동안 많은 사람들이 풀이를 구하려고 했으나 성공하지 못했고, 19세기에 들어와서 세 가지 문제 모두
작도가 불가능하다는 것이 증명되었다. 세 가지 문제는 다음과 같다.
주어진 각을 삼등분하는 문제[편집]
 이 부분의 본문은 각의 3등분입니다.
이 부분의 본문은 각의 3등분입니다.
주어진 정육면체의 2배 부피를 가지는 정육면체를 작도하는 문제[편집]
이 문제는 흔히 델로스의
문제라고도 부른다. 전설에 따르면 기원전 430년, 아테네 시민들이 전염병을 없애려면 어떻게 해야
하냐고 델로스의 아폴로 신탁에 물었을 때, '제단을 두 배로 만들라'는 답을 들었다고 한다. 이에 아테네 시민들이
제단의 각 변을 두 배로 늘려서 만들었는데도, 전염병이 수그러들지 않았다. 왜냐하면 신탁의 답변은 제단의 길이를 두 배로 늘리는 것이 아니라
제단의 부피를 두 배로 늘리라는 것이었기 때문이다. 제단의 길이를 두 배로 늘리면, 제단의 부피는 여덟 배(23)가
된다.
원래 정육면체의 부피를 V라고 한다면, 2V의
부피를 가지는 정육면체는 원래 정육면체보다 변의 길이가 ![\sqrt[3]{2}](http://upload.wikimedia.org/math/6/2/f/62f6a0ce6cf44d89c6f3b211c98c43bd.png) 배가
되어야 한다.
배가
되어야 한다. ![\sqrt[3]{2}](http://upload.wikimedia.org/math/6/2/f/62f6a0ce6cf44d89c6f3b211c98c43bd.png) 는
작도 가능한 수가 아니므로, 이 문제는 눈금없는
자와 컴퍼스로는 해결할 수 없다.
는
작도 가능한 수가 아니므로, 이 문제는 눈금없는
자와 컴퍼스로는 해결할 수 없다.
![\sqrt[3]{2}](http://upload.wikimedia.org/math/6/2/f/62f6a0ce6cf44d89c6f3b211c98c43bd.png) 배가
되어야 한다.
배가
되어야 한다. ![\sqrt[3]{2}](http://upload.wikimedia.org/math/6/2/f/62f6a0ce6cf44d89c6f3b211c98c43bd.png) 는
작도 가능한 수가 아니므로, 이 문제는 눈금없는
자와 컴퍼스로는 해결할 수 없다.
는
작도 가능한 수가 아니므로, 이 문제는 눈금없는
자와 컴퍼스로는 해결할 수 없다.
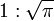 와
같은 비율을 만들 수 없기 때문에 이 문제는 해결이 불가능하다.
와
같은 비율을 만들 수 없기 때문에 이 문제는 해결이 불가능하다.
댓글 없음:
댓글 쓰기