Compass-and-straightedge or
ruler-and-compass construction is the construction of lengths, angles, and other geometric figures using only an
idealized ruler and compass.
The idealized ruler,
known as a straightedge, is assumed to be infinite in length,
and has no markings on it and only one edge. The compass is assumed to collapse
when lifted from the page, so may not be directly used to transfer distances.
(This is an unimportant restriction, as this may be achieved via the compass equivalence
theorem.) More formally, the only permissible constructions are
those granted by Euclid's first three
postulates.
Every point constructible
using straightedge and compass may be constructed using compass alone. A number
of ancient problems in plane geometry impose this
restriction.
The most famous
straightedge-and-compass problems have been proven impossible in several cases
by Pierre Wantzel in 1837,
using the mathematical theory of fields. In spite
of existing proofs of impossibility, some persist in trying to solve these
problems.[1] Many of these
problems are easily solvable provided that other geometric transformations are
allowed: for example, doubling the cube is possible using geometric
constructions, but not possible using straightedge and compass alone.
Creating a regular hexagon with a ruler and compass
Each construction must terminate. That is, it must have a finite number of steps, and not be the limit of ever closer approximations.
All compass and straightedge constructions consist of repeated application of
five basic constructions using the points, lines and circles that have already
been constructed. These are:
Compass and straightedge tools[edit]
The "compass" and "straightedge" of compass and straightedge constructions are idealizations of rulers and compasses in the real world:- The compass can be opened arbitrarily wide, but (unlike some real compasses) it has no markings on it. Circles can only be drawn starting from two given points: the centre and a point on the circle. The compass collapses when it's not drawing a circle, so it cannot be used to copy a length to another place.
- The straightedge is infinitely long, but it has no markings on it and has only one edge, unlike ordinary rulers. It can only be used to draw a line segment between two points or to extend an existing line.
The modern compass
generally does not collapse and several modern constructions use this feature.
It would appear that the modern compass is a "more powerful" instrument than the
ancient compass. However, by Proposition 2 of Book 1 of Euclid's Elements, no computational power is lost
by using such a collapsing compass; there is no need to transfer a distance from
one location to another. Although the proposition is correct, its proofs have a
long and checkered history.[2]
Each construction must be exact. "Eyeballing" it (essentially looking
at the construction and guessing at its accuracy, or using some form of
measurement, such as the units of measure on a ruler) and getting close does not
count as a solution.Each construction must terminate. That is, it must have a finite number of steps, and not be the limit of ever closer approximations.
Stated this way, compass
and straightedge constructions appear to be a parlour game, rather than a serious practical
problem; but the purpose of the restriction is to ensure that constructions can
be proven to be exactly correct, and is thus important to both
drafting (design by both CAD software and traditional drafting with pencil,
paper, straight-edge and compass) and the science of weights and measures, in
which exact synthesis from reference bodies or materials is extremely
important.[citation needed] One of the chief
purposes of Greek mathematics was to find exact constructions for various
lengths; for example, the side of a pentagon inscribed in a given circle. The Greeks
could not find constructions for three problems:
- Squaring the circle: Drawing a square the same area as a given circle.
- Doubling the cube: Drawing a cube with twice the volume of a given cube.
- Trisecting the angle: Dividing a given angle into three smaller angles all of the same size.
The basic constructions[edit]
All compass and straightedge constructions consist of repeated application of
five basic constructions using the points, lines and circles that have already
been constructed. These are:
- Creating the line through two existing points
- Creating the circle through one point with centre another point
- Creating the point which is the intersection of two existing, non-parallel
lines
- Creating the one or two points in the intersection of a line and a circle
(if they intersect)
- Creating the one or two points in the intersection of two circles (if they
intersect).
For example, starting with just two distinct points, we can create a line or
either of two circles (in turn, using each point as centre and passing through
the other point). If we draw both circles, two new points are created at their
intersections. Drawing lines between the two original points and one of these
new points completes the construction of an equilateral triangle.
Therefore, in any
geometric problem we have an initial set of symbols (points and lines), an
algorithm, and some results. From this perspective, geometry is equivalent to an
axiomatic algebra, replacing its elements by symbols.
Probably Gauss first realized this, and used it to prove the
impossibility of some constructions; only much later did Hilbert find a complete set
of axioms for geometry.
Constructible points and lengths[edit]
Formal proof[edit]
There are many different
ways to prove something is impossible. A more rigorous proof would be to
demarcate the limit of the possible, and show that to solve these problems one
must transgress that limit. Much of what can be constructed is covered in intercept theory.
We could associate an
algebra to our geometry using a Cartesian coordinate system
made of two lines, and represent points of our plane by vectors. Finally we can write these vectors as
complex numbers.
Using the equations for
lines and circles, one can show that the points at which they intersect lie in a
quadratic extension of the
smallest field F containing two points on the line, the center of the
circle, and the radius of the circle. That is, they are of the form  ,
where x, y, and k are in F.
Since the field of
constructible points is closed under square roots, it contains all points
that can be obtained by a finite sequence of quadratic extensions of the field
of complex numbers with rational coefficients. By the above paragraph, one can
show that any constructible point can be obtained by such a sequence of
extensions. As a corollary of this, one finds that the degree of the minimal
polynomial for a constructible point (and therefore of any constructible length)
is a power of 2. In particular, any constructible point (or length) is an algebraic number, though not
every algebraic number is constructible (i.e. the relationship between
constructible lengths and algebraic numbers is not bijective); for example,
,
where x, y, and k are in F.
Since the field of
constructible points is closed under square roots, it contains all points
that can be obtained by a finite sequence of quadratic extensions of the field
of complex numbers with rational coefficients. By the above paragraph, one can
show that any constructible point can be obtained by such a sequence of
extensions. As a corollary of this, one finds that the degree of the minimal
polynomial for a constructible point (and therefore of any constructible length)
is a power of 2. In particular, any constructible point (or length) is an algebraic number, though not
every algebraic number is constructible (i.e. the relationship between
constructible lengths and algebraic numbers is not bijective); for example, ![\sqrt[3]{2}](http://upload.wikimedia.org/math/6/2/f/62f6a0ce6cf44d89c6f3b211c98c43bd.png) is algebraic but not constructible.
is algebraic but not constructible.
 ,
where x, y, and k are in F.
,
where x, y, and k are in F.![\sqrt[3]{2}](http://upload.wikimedia.org/math/6/2/f/62f6a0ce6cf44d89c6f3b211c98c43bd.png) is algebraic but not constructible.
is algebraic but not constructible.Constructible angles[edit]
There is a bijection between the angles
that are constructible and the points that are constructible on any
constructible circle. The angles that are constructible form an abelian group under addition
modulo 2π (which corresponds to multiplication of the points on the unit circle
viewed as complex numbers). The angles that are constructible are exactly those
whose tangent (or equivalently, sine or cosine) is constructible as a number.
For example the regular heptadecagon (the seventeen-sided regular polygon) is
constructible because
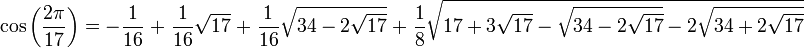
The group of
constructible angles is closed under the operation that halves angles (which
corresponds to taking square roots). The only angles of finite order that may be
constructed starting with two points are those whose order is either a power of
two, or a product of a power of two and a set of distinct Fermat primes. In addition
there is a dense set of constructible angles of infinite order.
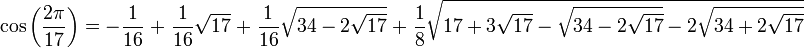
Compass and straightedge constructions as complex arithmetic[edit]
Given a set of points in
the Euclidean plane, selecting any one of them to be
called 0 and another to be called 1, together with an arbitrary
choice of orientation allows us to
consider the points as a set of complex numbers.
Given any such
interpretation of a set of points as complex numbers, the points constructible
using valid compass and straightedge constructions alone are precisely the
elements of the smallest field containing the original set of points and
closed under the complex conjugate and square root operations (to avoid ambiguity, we can
specify the square root with complex argument less than π). The elements of this
field are precisely those that may be expressed as a formula in the original
points using only the operations of addition, subtraction, multiplication, division, complex conjugate, and square root, which is easily
seen to be a countable dense subset of the plane. Each of these six operations
corresponding to a simple compass and straightedge construction. From such a
formula it is straightforward to produce a construction of the corresponding
point by combining the constructions for each of the arithmetic operations. More
efficient constructions of a particular set of points correspond to shortcuts in
such calculations.
Equivalently (and with no need to arbitrarily choose two points) we can say
that, given an arbitrary choice of orientation, a set of points determines a set
of complex ratios given by the ratios of the differences between any two pairs
of points. The set of ratios constructible using compass and straightedge from
such a set of ratios is precisely the smallest field containing the original
ratios and closed under taking complex conjugates and square roots.
For example the real part, imaginary part and modulus of a point or ratio
z (taking one of the two viewpoints above) are constructible as these may
be expressed as
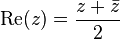


Doubling the cube
and trisection of an angle (except for special angles such as any
φ such that φ/6π is a rational number with denominator the product of a
power of two and a set of distinct Fermat primes) require ratios which are the
solution to cubic equations, while squaring the circle
requires a transcendental ratio. None of these are in the
fields described, hence no compass and straightedge construction for these
exists.
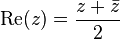


Impossible constructions[edit]
The following three construction problems, whose origins date from Greek
antiquity, were considered impossible in the sense that they could not be
solved using only the compass and straightedge. With modern mathematical methods
this "consideration" of the Greek mathematicians can be proved to be correct.
The problems themselves, however, are solvable, and the Greeks knew how to solve
them, without the constraint of working only with straightedge and
compass.
Squaring the circle[edit]
Main article: Squaring the circle
The most famous of these
problems, squaring the circle, otherwise known as the
quadrature of the circle, involves constructing a square with the same
area as a given circle using only straightedge and compass.
Squaring the circle has
been proven impossible, as it involves generating a transcendental number, that is, 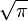 .
Only certain algebraic numbers can be constructed with ruler and
compass alone, namely those constructed from the integers with a finite sequence
of operations of addition, subtraction, multiplication, division, and taking
square roots. The phrase "squaring the circle" is often used to mean "doing the
impossible" for this reason.
Without the constraint of requiring solution by ruler and compass alone, the
problem is easily solvable by a wide variety of geometric and algebraic means,
and has been solved many times in antiquity.
.
Only certain algebraic numbers can be constructed with ruler and
compass alone, namely those constructed from the integers with a finite sequence
of operations of addition, subtraction, multiplication, division, and taking
square roots. The phrase "squaring the circle" is often used to mean "doing the
impossible" for this reason.
Without the constraint of requiring solution by ruler and compass alone, the
problem is easily solvable by a wide variety of geometric and algebraic means,
and has been solved many times in antiquity.
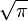 .
Only certain algebraic numbers can be constructed with ruler and
compass alone, namely those constructed from the integers with a finite sequence
of operations of addition, subtraction, multiplication, division, and taking
square roots. The phrase "squaring the circle" is often used to mean "doing the
impossible" for this reason.
.
Only certain algebraic numbers can be constructed with ruler and
compass alone, namely those constructed from the integers with a finite sequence
of operations of addition, subtraction, multiplication, division, and taking
square roots. The phrase "squaring the circle" is often used to mean "doing the
impossible" for this reason.





댓글 없음:
댓글 쓰기