In fact, in mathematics the “curvature” of a curve is usually defined as the “reciprocal of the radius of the osculating circle”. This is fancy talk for: fit a circle into the curve as best you can, then measure the radius of that circle, and flip it over.
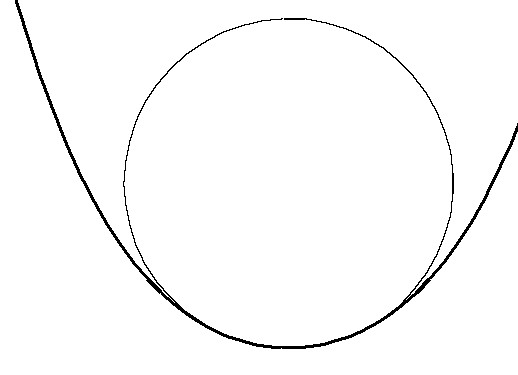
At any given point the osculating (or "kissing") circle
is the circle that fits a curve as closely as possible.
It makes sense; a smaller
circle should have a higher curvature (it’s turning faster) but it has a smaller
radius, R. So, use 1/R, which is big when R is small, and small when R is big.
There are some more technical reasons to use 1/R (like that you can apply it
directly to calculating the centrifugal force on a point following that path, or
that it gives rise to the entirely kick-ass Descartes’
theorem), but really it’s just one of the more reasonable
definitions.
So, just working with the standard definition, you say: the curvature of a circle is 1/R, if I let the radius become infinite, the curvature must go to zero. Zero curvature means no bending of any kind. Must be a line.
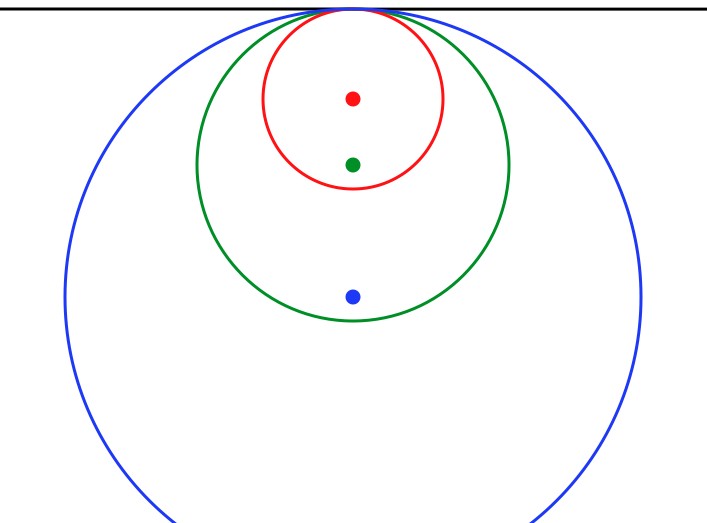
Nail down the edge of a circle. As the center gets
farther and farther away, the radius gets larger, and the curvature gets
smaller. When the "circle is centered at infinity" the curvature drops to zero,
and the edge becomes a straight line (black).
Old school topologists get very excited about this stuff.
Say you have two lines on a plane. They’ll always intersect at exactly one point, unless they’re parallel in which case they’ll never intersect at all. But the Greek Geometers, back in the day, didn’t like that; they wanted a more universal theorem. So they included the “line at infinity” with their plane, and created the “projective plane”. In so doing they created a new space where every pair of straight lines intersect at one point, no matter what.
To picture this, imagine the ground under your feet as the plane and the horizon as the line-at-infinity.

The tracks are parallel, so they'll never meet. But,
they look like they meet at the horizon. So why not (mathematically speaking)
"include" the horizon and define that as the place where the tracks
meet?
Parallel lines meet at two points on the horizon (in opposite directions). So the line at infinity is weirdly defined with opposite points on the horizon being the same point. Mathematicians would say “antipodal points are identified”. In the projective plane two lines always meet at one point.
Notice that east-west
parallel lines meet at the east-west point on the line at infinity, and
north-south parallel lines meet at the north-south point at infinity. So you
do need the entire horizon, not just a single “far away point”. A single point would yield the Riemann
sphere, which is also good times.
Back to the point. If you think about circles in this new-fangled projective plane, one of the first questions that comes to mind is “what happens if the circle includes a point on the line at infinity?”.
No matter how big the circle is, or where its center is, the whole thing will always be in the plane (not all the way out to the line at infinity). If the circle does have a point on the horizon, then you’ll find that the center also has to be at infinity (if it’s in the plane, then it’ll be closer to some points on the circle than others, but the center point is the same distance to every point on the circle). Specifically, the center will be on the line at infinity exactly 90° away from where the circle intersects the line.
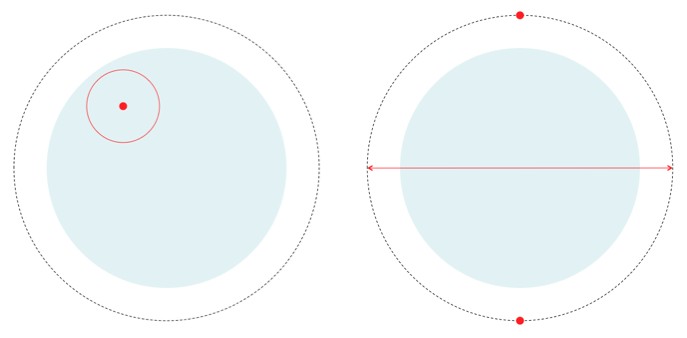
The projective plane, which includes the usual infinite
plane (light blue) and the line at infinity (dashed line), and two examples of
circles. Note that, although the plane is infinite, the line at infinity wraps
around it in the same way that the horizon would still wrap around you even if
the Earth were flat and infinite (this is an abstract picture). Left: a circle
and its center in the in the ordinary plane. Right: a circle that passes through
the east-west point on the line-at-infinity. Its center is at the north-south
point on the line-at-infinity.
This agrees surprisingly well with the intuition behind the more colorful circle picture above. Science and math truly are a beautiful tapestry of interconnections and nerding right the hell out.
Ask a Mathematician / Ask a Physicist
http://www.askamathematician.com
댓글 없음:
댓글 쓰기