What is the process of developing a picture of a higher dimensional object? |

How can we have any idea what a 4D hypercube or any n-D object “looks like”?



A picture of a 3D object is a “projection” of that object onto a 2D page. Projection to an artist means taking a picture or drawing a picture. To a mathematician it means keeping some dimensions and “pancaking” others.

So when you take a picture the “up/down” and “left/right” dimensions are retained, but the “forward/back” dimension is flattened. Mathematicians, being clever, have formalized this into a form that is independent of dimension. That is, you can take an object in any number of dimensions and “project out” any number of dimensions, until it’s something we can picture (3 or fewer dimensions).

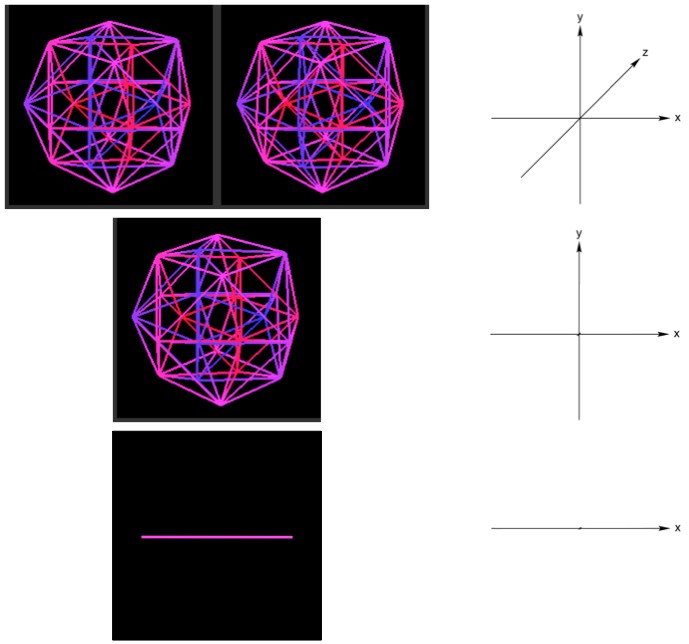
Top: An object in 3 dimensions. To see it, cross your eyes by looking “through” the screen until the two images line up. Middle: By “projecting out” the z axis (toward/away) the object is collapsed into two dimensions. This is what cameras do. Bottom: By projecting out the y axis (up/down) the object is collapsed again into 1 dimension. This is akin to what a 2D camera would see, photographing from below.

We’re used to a 3D-to-2D projection (it’s what our eyeballs do). A 4D-to-2D projection, like in the picture above, would involve 2 “camera/eyeball like” projections, so it’s not as simple as “seeing” a 4D object.

As for knowing what a 4D, 5D, … shape is, we just describe its properties mathematically, and solve. It’s necessary to use math to describe things that can’t be otherwise pictured or understood directly. If we had to completely understand modern physics to use it, we’d be up shit creek. However, by describing things mathematically, and then following the calculations to their conclusions, we can get a lot farther than our puny minds might otherwise allow.

Lines, squares, cubes, hyper-cubes, hyper-hyper-cubes, etc. all follow from each other pretty naturally. The 4D picture (being 4D) should be difficult to understand.

For example, to describe a hypercube you start with a line (all shapes are lines in 1D).

To go to 2D, you’d slide the line in a new direction (the 2nd dimension) and pick up all the points the line covers. Now you’ve got a square.

To go to 3D, you’d slide the square in a new direction (the 3rd dimension) and pick up all the points the square covers. Cube!

To go to 4D, same thing: slide the cube in the new (4th) direction. The only difference between this and all the previous times is that we can no longer picture the process. However, mathematically speaking, it’s nothing special.

---

Answer gravy: This isn’t more of an answer, it’s just an example of how, starting from a pattern in lower dimensions, you can talk about the properties of something in higher dimensions. In this case, the number of lines, faces, etc. that a hyper-cube will have in more than 3 dimensions.

Define as an N dimensional “surface”. So, is a point, is a line, is a square, is a cube, and so on.

Now define as the number of N-dimensional surfaces in a D-dimensional cube.
cube) has four corners, four edges, and one square.
The “slide, connect, and fill in” technique can be though of like this: when you slide a point it creates a line, when you slide a line it creates a square, when you slide a square it creates a cube, etc. Also, you find that you’ll have two copies of the original shape (picture above).

So, if you want to figure out how many “square pieces” you have in a D-dimensional cube you’d take the number of squares in a D-1 dimensional cube, double it (2 copies), and then add the number of lines in a D-1 dimensional cube (from sliding).

. Starting with a 0 dimensional cube (a point) you can safely define .

The values of e_N(D) arranged to make the pattern clearer. You can use the pattern to accurately predict what the cube in the next dimension will be like.

It’s neither obvious nor interesting how, but with a little mathing you’ll find that , where “!” means factorial. So, without ever having seen a hypercube, you can confidently talk about its properties! For example; a hypercube has 8 cubic “faces”, 24 square faces, 32 edges, and 16 corners.

Ask a Mathematician / Ask a Physicist

http://www.askamathematician.com