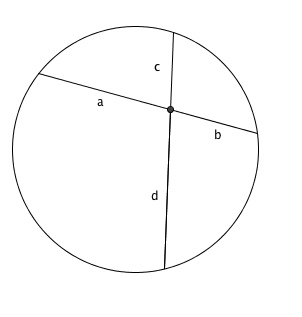
Mathematician: The Intersecting Chords theorem asks us to
consider two intersecting line segments inside of a circle (such that each line
segment starts and ends on the edge of the circle). Each line segment can be
thought of as being divided in two parts by the point where the two line
segments intersect (in the image below these parts are a and b for the first
line segment, and c and d for the second line segment). The Intersecting Chord
theorem says that when we multiply the lengths of the two parts of the first
line segment together, we get the same value as when we multiply the lengths of
the two parts of the other line segment together (that is, that a*b = c*d). The
Power of a Point theorem generalizes this situation to the case where only one
side of each line segment lies on the circle, and the other sides of the line
segments can intersect each other outside of the circle. The answer you get is a
bit different in this case.
One way to think about why the Intersecting Chords theorem is true is because
the triangle formed with a and d as two of its sides is a similar triangle to
(has the same angles as) the triangle formed that has c and b as two of it’s
sides. Because the triangles are similar, that implies that a/d = c/b (that
is, the ratio of side lengths should be the same for the two triangles), and if
we multiply both sides of this equation by both b and d, we get a b = c d
which is just the Intersecting Chord Theorem.
For more info see:

댓글 없음:
댓글 쓰기