녹원학원 수학과학영재교육 010-3549-5206 : What’s so special about the Gaussian distribution (i.e. the normal distribution / bell curve)??

2013년 10월 22일 화요일

What’s so special about the Gaussian distribution (i.e. the normal distribution / bell curve)??

Physicist: A big part of what makes physicists slothful and attractive is a theorem called the “central limit theorem”. In a nutshell it says that, even if you can’t describe how a single random thing happens, a whole mess of them together will act like a gaussian. If you have a weighted die I won’t be able to tell you the probability of each individual number being rolled. But (given the mean and variance) if you roll a couple dozen weighted dice and add them up I can tell you (with fairly small error) the probability of any sum, and the more dice the smaller the error. Systems with lots of pieces added together show up all the time in practice, so knowing your way around a gaussian is well worth the trouble.

Gaussians also maximize entropy for a given energy (or other conserved quadratic quantity, energy is quadratic because $E = \frac{1}{2} mv^2$ ). So if you have a bottle of gas at a given temperature (which fixes the total energy) you’ll find that the probability that a given particle is moving with a given velocity is given by a gaussian distribution.

From quantum mechanics, gaussians are the most “certain” wave functions. The “Heisenberg uncertainty principle” states that for any wave function $\Delta X \Delta P \ge \frac{\hbar}{2}$ , where $\Delta X$ is the uncertainty in position and $\Delta P$ is the uncertainty in momentum. For a gaussian: $\Delta X \Delta P = \frac{\hbar}{2}$ , the absolute minimum total uncertainty.

And much more generally, we know a lot about gaussians and there’s a lot of slick, easy math that works best on them. So whenever you see a “bump” a good gut reaction is to pretend that it’s a “gaussian bump” just to make the math easier. Sometimes this doesn’t work, but often it does or it points you in the right direction.

Mathematician: I’ll add a few more comments about the Gaussian distribution (also known as the normal distribution or bell curve) that the physicist didn’t explicitly touch on. First of all, while it is an extremely important distribution that arises a lot in real world applications, there are plenty of phenomenon that it does not model well. In particular, when the central limit theorem does not apply (i.e. our data points were not produced by taking a sum or average over samples drawn from more or less independent distributions) and we have no reason to believe our distribution should have maximum entropy, the normal distribution is the exception rather than the rule.

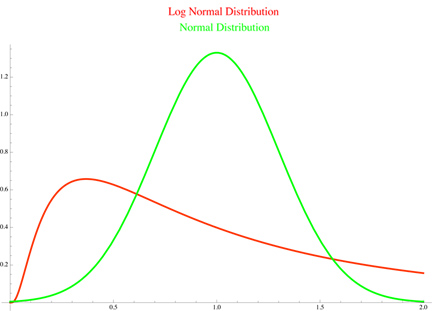
To give just one of many, many examples where non-normality arises: when we are dealing with a product (or geometric mean) of (essentially independent) random variables rather than a sum of them, we should expect that the resulting distribution will be approximately log-normal rather than normal (see image below). As it turns out, daily returns in the stock market are generally better modeled using a log-normal distribution rather than a normal distribution (perhaps this is the case because the most a stock can lose in one day is -100%, whereas the normal distribution assigns a positive probability to all real numbers). There are, of course, tons of other distributions that arise in real world problems that don’t look normal at all (e.g. the exponential distribution, Laplace distribution, Cauchy distribution, gamma distribution, and so on.)

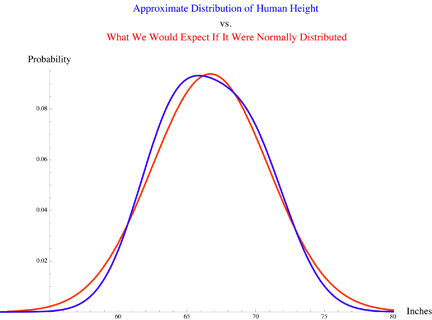
Human height provides an interesting case study, as we get distributions that are almost (but not quite) normally distributed. The heights of males (ignoring outliers) are close to being normal (perhaps height is the result of a sum of a number of nearly independent factors relating to genes, health, diet, etc.). On the other hand, the distribution of heights of people in general (i.e. both males and females together) looks more like the sum of two normal distributions (one for each gender), which in this case is like a slightly skewed normal distribution with a flattened top.

I’ll end with a couple more interesting facts about the normal distribution. In Fourier analysis we observe that, when it has an appropriate variance, the normal distribution is one of the eigenvectors of the Fourier transform operator. That is a fancy way of saying that the gaussian distribution represents its own frequency components. For instance, we have this nifty equation (relating a normal distribution to its Fourier transform):

$e^{- \pi x^2}=\int_{-\infty}^{\infty} e^{- \pi s^2}e^{-2 \pi i s x} ds$ .

Note that the general equation for a (1 dimensional) Gaussian distribution (which tells us the likelihood of each value x) is

$\frac{ e^{- \frac{(x-\mu)^2}{2 \sigma^2}} } {\sqrt{2 \pi \sigma^2}}$

where $\mu$ is the mean of the distribution, and $\sigma$ is its standard deviation. Hence, the Fourier transform relation above deals with a normal distribution of mean 0 and standard deviation $\frac{1}{\sqrt{2 \pi}}$ .

Another useful property to take note of relates to solving maximum likelihood problems (where we are looking for the parameters that make some data set as likely as possible). We generally end up solving these problems by trying to maximize something related to the log of the probability distribution under consideration. If we use a normal distribution, this takes the unusually simple form

$\log{ \frac{ e^{- \frac{(x-\mu)^2}{2 \sigma^2}} } {\sqrt{2 \pi \sigma^2}} } = - \frac{(x-\mu)^2}{2 \sigma^2} - \frac{1}{2} \log(2 \pi \sigma^2)$

which is often nice enough to allow for solutions that can be calculated exactly by hand. In particular, the fact that this function is quadratic in x makes it especially convenient, which is one reason that the Gaussian is commonly chosen in statistical modeling. In fact, the incredibly popular ordinary least squares regression technique can be thought of as finding the most likely line (or plane, or hyperplane) to fit a dataset, under the assumption that the data was generated by a linear equation with additive gaussian noise.

Ask a Mathematician / Ask a Physicist

댓글 없음:

댓글 쓰기