피보나치 수는
수학에서 아래의
점화식으로 정의되는
수열이다.

피보나치 수는 0과 1로 시작하며, 다음 피보나치 수는 바로 앞의 두 피보나치 수의 합이 된다.
n = 0, 1,...에 해당하는 피보나치 수는 (
OEIS의 수열
A000045)
- 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597, 2584, 4181, 6765, 10946...
이다.
역사
피보나치 수가 처음 언급된 문헌은
기원전 5세기 인도의
수학자 핑갈라가 쓴 책이다. 한편
유럽에서 피보나치 수를 처음 연구한 것은
레오나르도 피보나치로
토끼 수의 증가에 대해서 이야기하면서 이 수에 대해 언급했다.
n 번째 달의 토끼 수는
- 첫 달에는 새로 태어난 토끼 한 쌍만이 존재한다.
- 두 달 이상이 된 토끼는 번식 가능하다.
- 번식 가능한 토끼 한 쌍은 매달 새끼 한 쌍을 낳는다.
- 토끼는 죽지 않는다.
따라서 첫 달에는 새로 태어난 토끼 한 쌍이 있고, 두 번째 달에는 그대로 토끼 한 쌍, 세 번째 달부터는 이 토끼 한 쌍이 새끼를 낳게 되어 토끼가 2쌍이 되고, 네 번째 달에는 3쌍, 다섯 번째 달에는 5쌍이 된다. 이때
n번째 달에
a 쌍의 토끼가 있었고, 다음
n+1 번째 달에는 새로 태어난 토끼를 포함해
b 쌍이 있었다고 하자. 그러면 그다음
n+2 번째 달에는
a+
b 쌍의 토끼가 있게 된다. 이는
n번째 달에 살아있던 토끼는 충분한 나이가 되어 새끼를 낳을 수 있지만, 바로 전달인
n+1번째에 막 태어난 토끼는 아직 새끼를 낳을수 없기 때문이다.
피보나치 수의 성질
피보나치 수의
생성함수는

로 정리된다. 이 식으로부터 n번째 피보나치 수는 간단히
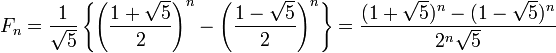
로 정리된다. 이 식은
오일러가
1765년 처음 발표했으나 잊혀졌다가,
1848년 비네에 의해 재발견되었다. 이 식을 비네의 식이라고 부른다.
황금비 값을

라 하면

라 적을 수도 있다.
피보나치 수의 정의를
음의 정수에 대해 확장할 수 있다. 음의 정수
-n에 대해

라 정의하면 이 값은 위의 점화식과 비네의 식을 모두 만족한다.
또한, 피보나치 수열은 서로 인접한 항끼리
서로 소이다. 이것은 귀납법으로 간단히 증명할 수 있다.
피보나치 수 구하기
피보나치 수를 위의 황금비 값의 거듭제곱으로 구하는 것은 계산오차 때문에 좋지 않다. 피보나치 수를 컴퓨터 등에서 구할 때는 0번째와 1번째 값부터 차례대로 앞의 두 값을 더해서 얻는 것이 좋다.
큰
n 값에 대해서는 다음의
행렬 연산식을 이용해서 빨리 구할 수 있다.

피보나치 수를 구하는 실제 코드는
피보나치 수 프로그램을 참고하라.
항등식
 라 하면
라 하면


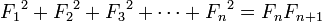
 (카시니의 항등식)
(카시니의 항등식)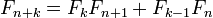





댓글 없음:
댓글 쓰기